题目内容
已知等比数列{an}的公比q<0,其前n项和为Sn,则a10S9与a9S10的大小关系是( )
| A、a10S9>a9S10 |
| B、a10S9<a9S10 |
| C、a10S9=a9S10 |
| D、a10S9与a9S10的大小关系与a1的值有关 |
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:将两个式子作差,利用等比数列的前n项和公式及通项公式将差变形,能判断出差的符号,从而得到两个数的大小.
解答:
解:因为等比数列{an}的公比q<0,
所以a10S9-a9S10=
•a1q9-
•a1q8
=-a12q8<0,
所以a10S9<a9S10.
故选:B.
所以a10S9-a9S10=
| a1(1-q9) |
| 1-q |
| a1(1-q10) |
| 1-q |
=-a12q8<0,
所以a10S9<a9S10.
故选:B.
点评:解决比较数的大小的题目,一般利用作差比较或作商比较,关键是将差或商变形.

练习册系列答案
相关题目
若关于x的方程x2+4x+|m-1|+2|m|=0(m∈R)有实根,则m的取值范围是( )
A、m≥
| ||
| B、-1≤m≤0 | ||
C、-1≤m≤
| ||
D、0≤m≤
|
已知直线l:mx-y-m+1=0(m∈R),若存在实数m,使得直线l被曲线C所截得的线段长度为|m|,则称曲线C为l的“优美曲线”.下面给出的曲线:
①y=-|x-1|;
②(x-1)2+(y-1)2=1;
③x2+3y2=4.
其中是直线l的“优美曲线”的有( )
①y=-|x-1|;
②(x-1)2+(y-1)2=1;
③x2+3y2=4.
其中是直线l的“优美曲线”的有( )
| A、①② | B、③ | C、②③ | D、①②③ |
在△ABC中,A,∠B,∠C所对的边分别为a,b,c,若cos2B+cosB+cos(A-C)=1,则下列说法正确的是( )
| A、a,b,c三边成等比数列 |
| B、a,b,c三边成等差数列 |
| C、a,c,b三边成等比数列 |
| D、a,c,b三边成等差数列 |
曲线C:f(x,y)=0关于直线l:x-y-3=0的对称曲线C′的方程是( )
| A、f(x-3,y)=0 |
| B、f(y+3,x)=0 |
| C、f(y-3,x+3)=0 |
| D、f(y+3,x-3)=0 |
已知i为虚数单位,z=
,且z的共轭复数为
,则
=( )
| 1 |
| 1-i |
. |
| z |
. |
| z |
A、
| ||
B、
| ||
| C、1+i | ||
| D、1-i |
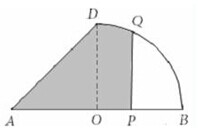 如图,△ABD是一直角边为1的直角等腰三角形,平面图形OBD是四分之一圆的扇形,点P在线段AB上,PQ⊥AB,且PQ交AD或交弧DB于点Q,设AP=x(0<x<2),图中阴影部分这平面图形APQ(或APQD)的面积为y,则函数y=f(x)的大致图象是( )
如图,△ABD是一直角边为1的直角等腰三角形,平面图形OBD是四分之一圆的扇形,点P在线段AB上,PQ⊥AB,且PQ交AD或交弧DB于点Q,设AP=x(0<x<2),图中阴影部分这平面图形APQ(或APQD)的面积为y,则函数y=f(x)的大致图象是( )


