题目内容
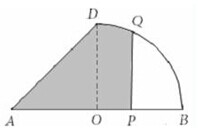 如图,△ABD是一直角边为1的直角等腰三角形,平面图形OBD是四分之一圆的扇形,点P在线段AB上,PQ⊥AB,且PQ交AD或交弧DB于点Q,设AP=x(0<x<2),图中阴影部分这平面图形APQ(或APQD)的面积为y,则函数y=f(x)的大致图象是( )
如图,△ABD是一直角边为1的直角等腰三角形,平面图形OBD是四分之一圆的扇形,点P在线段AB上,PQ⊥AB,且PQ交AD或交弧DB于点Q,设AP=x(0<x<2),图中阴影部分这平面图形APQ(或APQD)的面积为y,则函数y=f(x)的大致图象是( )A、 |
B、 |
C、 |
D、 |
考点:函数的图象
专题:函数的性质及应用
分析:分两段,当P点在A0之间时,当P点在OB之间时,再有二次函数的性质可知.
解答:
解:当P点在A0之间时,f(x)=
x2(0<x≤1),当P点在OB之间时,设∠QOP=θ,f(x)=
+
-[(
πθ-
(x-1)sinθ)],其中cosθ=
,
由二次函数的性质可知,只有A符合,
故选:A.
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x-1 |
由二次函数的性质可知,只有A符合,
故选:A.
点评:本题主要考查了二次函数的图象的性质,属于基础题.

练习册系列答案
相关题目
在(x-y)11的展开式中,各项系数的和为( )
| A、0 |
| B、211 |
| C、1 |
| D、210 |
已知函数f(x)=cosx+sinα,f′(
)=( )
| π |
| 2 |
| A、0 | B、1 | C、-1 | D、2 |
已知等比数列{an}的公比q<0,其前n项和为Sn,则a10S9与a9S10的大小关系是( )
| A、a10S9>a9S10 |
| B、a10S9<a9S10 |
| C、a10S9=a9S10 |
| D、a10S9与a9S10的大小关系与a1的值有关 |
若p=
+
,q=
+
,则p,q的大小关系是( )
| 2 |
| 5 |
| 3 |
| 4 |
| A、p<q | B、p=q |
| C、p>q | D、无法确定 |
| lim |
| △x→0 |
| f(x0-2△x)-f(x0) |
| 3△x |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
用反证法证明:如果a>b>0,则
>
.其中假设的内容应是( )
| a |
| b |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|