以下五个命题：
（1）不共面的四点中，其中任意三点不共线；
（2）垂直同一条直线的两条直线互相平行；
（3）平行于同一条直线的两条直线互相平行；
（4）若直线a，b共面，直线a，c共面，则直线b，c共面；
（5）依次首尾相接的四条线段必共面．
其中正确命题的个数是（　　）
A、1B、2C、3D、4
（文科）在空间四边形SABC中，G是底面三角形ABC的重心，M是棱SA上的一点，若MG∥平面SBC，则SM：MA=（　　）
A、1：1B、2：1
C、1：2D、2：3
已知函数f（x）=2cos（2x+φ），（|φ|＜
π
2
，x∈R）的图象的一部分如图所示，为了得到函数f（x）的图象，只要将函数g（x）=2cos2x的图象上所有的点（　　）
A、向左平移
π
6
个单位长度
B、向右平移
π
6
个单位长度
C、向左平移
π
3
个单位长度
D、向右平移
π
3
个单位长度
已知函数f（x）=（x-a）2+（
2
x
-a）2-a2+2（x＞0，a∈R），若函数f（x）有四个不同的零点，则a的取值范围是（　　）
A、-3
2
＜a＜3
2
B、a＞3
2
C、2
2
＜a＜3
2
D、a＞2
2
设函数f（x）=
x-[x]，x＜0
f(x-1)，x≥0
，其中[x]表示不超过x的最大整数，如[-1.6]=-2，[1]=1，[1.2]=1，若直线y=kx+1（k＜0）与函数y=f（x）的图象恰有2个不同的交点，则k的取值范围是（　　）
A、[-
1
2
，-
1
3
）
B、[-1，-
1
2
）
C、（-1，-
1
2
]
D、（-
1
2
，-
1
3
]
已知f（x）=
x2+1(x≤0)
-2x(x＞0)
，若f（a）=10，则a的值为（　　）
A、-1B、1C、-3D、3
已知在△ABC中，
AR
=2
RB
，
CP
=2
PR
，若
AP
=m
AB
+n
AC
，则m+n=（　　）
A、1
B、
8
9
C、
7
9
D、
2
3
设a=0.60.4，b=0.40.6，c=0.40.4，则a，b，c的大小关系是（　　）
A、c＞a＞b
B、a＞b＞c
C、a＞c＞b
D、b＞c＞a
若向量
a
，
b
是一组基底，向量
c
=x
a
+y
b
（x，y∈R），则称（x，y）为向量
c
在基底
a
，
b
下的坐标．现已知向量
t
在基底
p
=（1，2），
q
=（-1，1）下的坐标为（-1，-3），则向量
t
在另一组基底
m
=（1，-1），
n
=（0，-1）下的坐标为（　　）
A、（-1，-3）
B、（2，-3）
C、（2，-5）
D、（2，3）
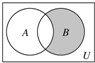已知全集U=N，A={0，1，2}，B={y|y=2x，x∈A}，则图中的阴影部分所表示的集合等于（　　）
A、{0}B、{2}
C、{4}D、{2，4}
 0  208417  208425  208431  208435  208441  208443  208447  208453  208455  208461  208467  208471  208473  208477  208483  208485  208491  208495  208497  208501  208503  208507  208509  208511  208512  208513  208515  208516  208517  208519  208521  208525  208527  208531  208533  208537  208543  208545  208551  208555  208557  208561  208567  208573  208575  208581  208585  208587  208593  208597  208603  208611  266669 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网