题目内容
已知在△ABC中，
=2
，
=2
，若
=m
+n
，则m+n=（ ）
| AR |
| RB |
| CP |
| PR |
| AP |
| AB |
| AC |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：如图所示，由于
=
+
，
=
，
=
+
，
=
，可得
=
+
．与
=m
+n
比较即可得出．
| AP |
| AC |
| CP |
| CP |
| 2 |
| 3 |
| CR |
| CR |
| CA |
| AR |
| AR |
| 2 |
| 3 |
| AB |
| AP |
| 1 |
| 3 |
| AC |
| 4 |
| 9 |
| AB |
| AP |
| AB |
| AC |
解答：
解：如图所示，
∵
=
+
，
=
，
=
+
，
=
，
∴
=
+
．
与
=m
+n
比较，可得：
m=
，n=
则m+n=
．
故选：C．
∵
| AP |
| AC |
| CP |
| CP |
| 2 |
| 3 |
| CR |
| CR |
| CA |
| AR |
| AR |
| 2 |
| 3 |
| AB |
∴
| AP |
| 1 |
| 3 |
| AC |
| 4 |
| 9 |
| AB |
与
| AP |
| AB |
| AC |
m=
| 4 |
| 9 |
| 1 |
| 3 |
则m+n=
| 7 |
| 9 |
故选：C．
点评：本题考查了向量的三角形法则、向量共线定理、共面向量基本定理，考查了推理能力和计算能力，属于中档题．
练习册系列答案
相关题目
已知适合不等式|x2-4x+p|+|x-3|≤5的x的最大值为3，则p的值为（ ）
| A、2 | B、4 | C、8 | D、12 |
f（x）={
，若f（a）+f（1）=0，则a的值等于（ ）
2x，x＞0 x+1，x≤0 |
| A、-3 | B、-1 | C、1 | D、3 |
要得到函数y=2sin（2x-
）的图象，只需要将函数y=2sin2x的图象向 平移 个单位．（ ）
| π |
| 2 |
A、左
| ||
B、右
| ||
C、左
| ||
D、右
|
下列判断错误的是（ ）
A、在△ABC中，“
| ||||||||||||
| B、命题“?x∈R，x2-x-1≤0”的否定是“?x0∈R，x02-x0-1＞0” | ||||||||||||
| C、若p，q均为假命题，则p∧q为假命题 | ||||||||||||
D、若向量
|
（文科）在空间四边形SABC中，G是底面三角形ABC的重心，M是棱SA上的一点，若MG∥平面SBC，则SM：MA=（ ）
| A、1：1 | B、2：1 |
| C、1：2 | D、2：3 |
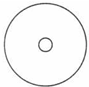如图，半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆，现将半径为1cm的一枚硬币拋到此纸板上，使整块硬币随机完全落在纸板内，则硬币与小圆无公共点的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
若两个函数的图象仅经过若干次平移后能够重合，则称这两个函数为“同形”函数．给出下列三个函数：f1（x）=
sin2x，f2（x）=sinx+cosx，f3（x）=
cos（x+
）+1，则（ ）
| 2 |
| 2 |
| π |
| 6 |
| A、f1（x），f2（x），f3（x）两两为“同形”函数 |
| B、f1（x），f2（x）为“同形”函数，且它们与f3（x）不为“同形”函数 |
| C、f2（x），f3（x）为“同形”函数，且它们与f1（x）不为“同形”函数 |
| D、f1（x），f2（x），f3（x）两两不为“同形”函数 |