题目内容
若向量
,
是一组基底,向量
=x
+y
(x,y∈R),则称(x,y)为向量
在基底
,
下的坐标.现已知向量
在基底
=(1,2),
=(-1,1)下的坐标为(-1,-3),则向量
在另一组基底
=(1,-1),
=(0,-1)下的坐标为( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| t |
| p |
| q |
| t |
| m |
| n |
| A、(-1,-3) |
| B、(2,-3) |
| C、(2,-5) |
| D、(2,3) |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:通过已知条件可以求出向量
的坐标,然后设
=x
+y
,带入坐标即可求得x,y,从而求出向量
在
,
下的坐标.
| t |
| t |
| m |
| n |
| t |
| m |
| n |
解答:
解:由已知条件知:
=-(1,2)-3(-1,1)=(2,-5);
设
=x
+y
,则:
解得:x=2,y=3.
向量
在基底
=(1,-1),
=(0,-1)下的坐标为:(2,3).
故选:D.
| t |
设
| t |
| m |
| n |
|
向量
| t |
| m |
| n |
故选:D.
点评:考查向量基底的概念,向量坐标的定义.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
和两条异面直线都平行的直线( )
| A、只有一条 | B、两条 |
| C、无数条 | D、不存在 |
三棱锥A-BCD的顶点A在底面BCD内的射影为点O,且点O到三个侧面的距离相等,则点O一定是△BCD的( )
| A、重心 | B、内心 | C、垂心 | D、外心 |
设m,n是不同的直线,α,β,γ是不同的平面,有以下四个命题:
①
⇒β∥γ
②
⇒m⊥β
③
⇒α⊥β
④
⇒m∥α
其中正确的个数( )
①
|
②
|
③
|
④
|
其中正确的个数( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知函数f(x)=(x-a)2+(
-a)2-a2+2(x>0,a∈R),若函数f(x)有四个不同的零点,则a的取值范围是( )
| 2 |
| x |
A、-3
| ||||
B、a>3
| ||||
C、2
| ||||
D、a>2
|
a=log70.3,b=0.37,c=70.3,则( )
| A、a<c<b |
| B、b<c<a |
| C、a<b<c |
| D、b<a<c |
设a,b为实数,则“a<
或b>
”是“0<ab<1”的( )
| 1 |
| b |
| 1 |
| a |
| A、充分条件但不是必要条件 |
| B、必要条件但不是充分条件 |
| C、既是充分条件,也是必要条件 |
| D、既不是充分条件,也不是必要条件 |





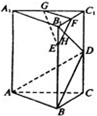 如图在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,E是BB1上的一点,且EB1=1,D、F、G分别是CC1、B1C1、A1C1的中点,EF与B1D相交于H.
如图在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=2,CC1=4,E是BB1上的一点,且EB1=1,D、F、G分别是CC1、B1C1、A1C1的中点,EF与B1D相交于H.