抛物线y2=4x的焦点为F,点A,B在抛物线上,且∠AFB=120°,弦AB中点M在其准线上的射影为N,则
的最大值为( )
| |MN| |
| |AB| |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
集合P={x|x+
≤2,x∈Z},集合Q={x|x2+2x-3>0},则P∩∁RQ=( )
| 1 |
| x |
| A、[-3,0) |
| B、{-3,-2,-1} |
| C、{-3,-2,-1,1} |
| D、{-3,-2,-1,0} |
命题“?x>0,x2+x>0”的否定是( )
| A、?x0>0,x02+x0>0 |
| B、?x0>0,x02+x0≤0 |
| C、?x>0,x2+x≤0 |
| D、?x≤0,x2+x>0 |
已知
是z的共轭复数,若z=1+i(i是虚数单位),则z•
=( )
. |
| z |
. |
| z |
| A、-2 | B、-1 | C、0 | D、2 |
观察图:
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
…
则第( )行的各数之和等于20112.
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
…
则第( )行的各数之和等于20112.
| A、2010 | B、2009 |
| C、1006 | D、1005 |
函数f(x)=sinx•ln(x2+1)的部分图象可能是( )
A、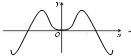 |
B、 |
C、 |
D、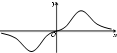 |
下列命题中是假命题的是( )
| A、不等式|x-3|+|x+1|<6的整数解有7个 |
| B、?a>0,f(x)=lnx-a有零点 |
| C、若y=f(x)的图象关于某点对称,那么?a,b∈R使得y=f(x-a)+b是奇函数 |
| D、?m∈R使f(x)=(m-1)•x m2-4m+3是幂函数,且在(0,+∞)上递减 |
若集合P={y|y≥0},P∩Q=Q,则集合Q不可能是( )
| A、∅ |
| B、{y|y=x2,x∈R} |
| C、{y|y=2x,x∈R} |
| D、{y|y=log2x,x>0} |
定义在R上的奇函数f(x)在(-∞,0)内有1005个零点,则函数f(x)的零点个数( )
| A、2009 | B、2010 |
| C、2011 | D、2012 |