题目内容
抛物线y2=4x的焦点为F，点A，B在抛物线上，且∠AFB=120°，弦AB中点M在其准线上的射影为N，则
的最大值为（ ）
| |MN| |
| |AB| |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：设AF=a，BF=b，由抛物线定义，2MN=a+b．再由余弦定理可得|AB|2=a2+b2-2abcos120°，进而根据a+b≥2
，求得|AB|的范围，进而可得答案．
| ab |
解答：
解：设AF=a，BF=b，由抛物线定义，2MN=a+b．
而余弦定理，|AB|2=a2+b2-2abcos120°=（a+b）2-ab，
再由a+b≥2
，得到|AB|≥
（a+b）．
所以
的最大值为
．
故选：A．
而余弦定理，|AB|2=a2+b2-2abcos120°=（a+b）2-ab，
再由a+b≥2
| ab |
| ||
| 2 |
所以
| |MN| |
| |AB| |
| ||
| 3 |
故选：A．
点评：本题主要考查抛物线的应用和余弦定理的应用．考查了学生综合分析问题和解决问题的能力．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
如图所示，A，B分别为椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| |MN|2 |
| |AM||BN| |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
今有10个大小相同的乒乓球都放在一个黑色的袋子里，其中4个球上标了数字1，3个球上标了数字2，剩下的球都标了数字5，现从中任取3个球，求所取的球数字总和超过8的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）=sinx•ln（x2+1）的部分图象可能是（ ）
A、 |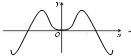
B、 |
C、 |
D、 |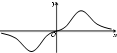
重庆某中学高二年级共有学生800名，现在从该校高二年级学生中随机抽取100名学生，将他们数学学业水平考试成绩分成6组：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]加以统计，得到如图所示的频率分布直方图．据此统计，该校高二年级学生数学学业水平考试成绩不低于及格分数（60分）的学生人数为（ ）| A、80 | B、100 |
| C、600 | D、640 |
设f（x）=3ax+1-2a在（-1，1）上存在x0使f（x0）=0，则实数a的取值范围是（ ）
A、a＜
| ||
B、a＞
| ||
C、a＞
| ||
| D、a＜-1 |