题目内容
函数f（x）=sinx•ln（x2+1）的部分图象可能是（ ）
A、 |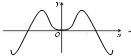
B、 |
C、 |
D、 |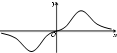
考点：函数的图象
专题：函数的性质及应用
分析：首先判断出函数为奇函数，再根据零点的个数判断，问题得以解决．
解答：
解：∵f（-x）=sin（-x）•ln（x2+1）=-（sinx•ln（x2+1））=-f（x），
∴函数f（x）为奇函数，图象关于原点对称，
∵sinx存在多个零点，
∴f（x）存在多个零点，
故f（x）的图象应为含有多个零点的奇函数图象．
故选B．
∴函数f（x）为奇函数，图象关于原点对称，
∵sinx存在多个零点，
∴f（x）存在多个零点，
故f（x）的图象应为含有多个零点的奇函数图象．
故选B．
点评：本题通过图象考查函数的奇偶性以及单调性，属于基础题．
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
设集合A={x∈R|x＞a}，若2∈A，则实数a的取值范围是（ ）
| A、a＜2 | B、a≤2 |
| C、a＞2 | D、a≥2 |
设m、n是两条不同的直线，α、β是两个不同的平面，若已知m⊥n，m⊥α，则“n⊥β”是“α⊥β”的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也必要条件 |
抛物线y2=4x的焦点为F，点A，B在抛物线上，且∠AFB=120°，弦AB中点M在其准线上的射影为N，则
的最大值为（ ）
| |MN| |
| |AB| |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
执行如图所示的程序框图，则输出的数的个数是（ ）
| A、7 | B、6 | C、5 | D、4 |
已知命题“p：?x＞0，lnx＜x”，则￢p为（ ）
| A、?x∈R，lnx≥x |
| B、?x＞0，lnx≥x |
| C、?x∈R，lnx＜x |
| D、?x＞0，lnx＜x |