一般信号塔越高覆盖区域越大,某地为测量信号覆盖区域,决定测量信号塔高度,某技术人员在C点测得信号塔在南偏西80°,塔顶仰角为45°,此人沿南偏东40°方向前进100米到D,测得塔顶A的仰角为30°,则信号塔高为( )
| A、150米 | B、50米 |
| C、100米 | D、120米 |
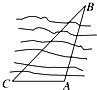 某地决定修建一条长为AB的跨河大桥,如图,A、B两点在河的两岸,一测量者在A的同侧,在所在的河岸边选定一点C,测得AC的距离为am,∠ACB=45°,∠CAB=105°,则A、B两点的距离为( )
某地决定修建一条长为AB的跨河大桥,如图,A、B两点在河的两岸,一测量者在A的同侧,在所在的河岸边选定一点C,测得AC的距离为am,∠ACB=45°,∠CAB=105°,则A、B两点的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
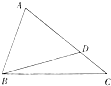 如图,在△ABC中,cos∠ABC=
如图,在△ABC中,cos∠ABC=