Question

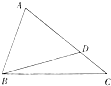如图，在△ABC中，cos∠ABC=

1

3

，AB=2，点D在线段AC上，且AD=2DC，BD=

4 3

3

．
求∠DBC的正弦值．

Answer 1

考点：正弦定理

专题：解三角形

分析：设BC=a，AD=2DC=2x，则AC=3x，通过余弦定理列出x与a的方程，由余弦定理分别求出∠ADB与∠BDC的余弦值，根据∠ADB+∠BDC=π得到a与x的关系是，联立两个方程求出x、a，然后求BCC、D的长，再由余弦定理求出cos∠DBC由平方关系求出∠DBC的正弦值．

解答： 解：设BC=a，AD=2DC=2x，则AC=3x，
在△ABC中，由余弦定理得，AC²=AB²+BC²-2AB•BCcos∠ABC
即9x²=4+a2-

4a

3

①，
在△ABD和△DBC中，由余弦定理得，
cos∠ADB=

BD2+AD2-AB2

2×BD×AD

=

16 3 +4x2-4

16 3 3 x

，
cos∠CDB=

BD2+CD2-BC2

2×BD×CD

=

16 3 +x2-a2

8 3 3 x

，

因为∠ADB+∠BDC=π，所以cos∠ADB=-cos∠BDC，
即

16 3 +4x2-4

16 3 3 x

=-

16 3 +x2-a2

8 3 3 x

，化简得3x²-a²=-6②…（8分）
由①②可得a=3，x=1，即BC=3，CD=1，
在△DBC中，由余弦定理得，
cos∠DBC=

BD2+BC2-CD2

2×BD×BC

=

16 3 +9-1

2× 4 3 3 ×3

=

5 3

9

，
所以sin∠DBC=

1-cos2∠CBD

=

6

9

．

点评：本题考查三角形中余弦定理的灵活应用，考查转化思想和方程思想，以及化简计算能力．