题目内容

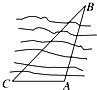某地决定修建一条长为AB的跨河大桥，如图，A、B两点在河的两岸，一测量者在A的同侧，在所在的河岸边选定一点C，测得AC的距离为am，∠ACB=45°，∠CAB=105°，则A、B两点的距离为（　　）
A、
2
am
B、
3
am
C、
2
2
am
D、
2
4
am
考点：正弦定理的应用
专题：计算题,解三角形
分析：由三角形内角和公式可得∠ABC=30°，再由正弦定理求出AB的值．
解答： 解：由三角形内角和公式可得∠ABC=30°，再由正弦定理可得
a
sin30°
=
AB
sin45°
，
解得 AB=
2
am，
故选A．
点评：本题主要考查正弦定理的应用，三角形的内角和公式，属于中档题．
练习册系列答案
相关题目
已知函数g（x）=
x2+ax+b
x
，x∈（0，+∞）．
（1）若g（x）在（0，1）上是减函数，在[1，+∞）上的增函数，求实数b的值；
（2）若（1）的条件下，若g（x）的最小值是1，求函数g（x）的解析式．
若△ABC的三边为a，b，c，它的面积为
a2+b2-c2
4
3
，那么内角C等于
 
．
（1）已知α，β都为锐角，sinα=
1
7
，cos（α+β）=
5
3
14
，求sinβ与cosβ的值；
（2）已知0＜β＜
π
2
＜α＜π，且cos（α-
β
2
）=-
1
9
，sin（
α
2
-β）=
2
3
，求cos（α+β）的值．
（1）已知tanσ=
1
2
，求
1+2sin(π-σ)cos(-2π-σ)
sin2(-σ)-sin2(
5π
2
-σ)
的值；
（2）已知sinσ+3cosσ=0，求sinσ，cosσ的值．
在△ABC中，角A，B，C的对边分别是a，b，c，若sinA=
3
sinC，B=30°，b=2，则△ABC的面积是（　　）
A、2
3
B、2
C、3
D、
3
执行如图的程序框图，如果输入的N是6，那么输出的p是（　　）
A、120B、720
C、1440D、5040
若复数z=（m2-2m）+（m2-m-2）i （m∈R）为纯虚数，则m的值为（　　）
A、0B、2C、0或2D、无解
已知|
a
|=4，|
b
|=8，|
a
+
b
|=4
3
．
（1）计算：
a
与
b
的夹角是θ；
（2）当k为何值时，（
a
+2
b
）⊥（k
a
-
b
）？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网