题目内容
在△ABC中,角A,B,C的对边分别是a,b,c,若sinA=
sinC,B=30°,b=2,则△ABC的面积是( )
| 3 |
A、2
| ||
| B、2 | ||
| C、3 | ||
D、
|
考点:正弦定理
专题:解三角形
分析:由正弦定理将sinA=
sinC化为a=
c,由余弦定理和条件求出a、c的值,代入三角形的铭记公式求解.
| 3 |
| 3 |
解答:
解:由正弦定理,sinA=
sinC化为a=
c,
由余弦定理得,b2=a2+c2-2accosB,
即4=3c2+c2-2×
c2×
,
化简得,c=2,a=2
,
△ABC的面积S△ABC=
acsinB=
×2×2
×
=
,
故选:D.
| 3 |
| 3 |
由余弦定理得,b2=a2+c2-2accosB,
即4=3c2+c2-2×
| 3 |
| ||
| 2 |
化简得,c=2,a=2
| 3 |
△ABC的面积S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
故选:D.
点评:本题考查正弦、余弦定理,以及三角形的面积公式,熟练掌握公式是解题的关键.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
下列函数中,为偶函数的是( )
A、f(x)=sin(
| ||
B、f(x)=cos(
| ||
C、f(x)=tan(
| ||
D、f(x)=sin(
|
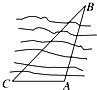 某地决定修建一条长为AB的跨河大桥,如图,A、B两点在河的两岸,一测量者在A的同侧,在所在的河岸边选定一点C,测得AC的距离为am,∠ACB=45°,∠CAB=105°,则A、B两点的距离为( )
某地决定修建一条长为AB的跨河大桥,如图,A、B两点在河的两岸,一测量者在A的同侧,在所在的河岸边选定一点C,测得AC的距离为am,∠ACB=45°,∠CAB=105°,则A、B两点的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
阅读如图的程序框图,运行相应的程序,则输出i的值为( )


| A、3 | B、4 | C、5 | D、6 |
已知an+1=2an+1 (n=1,2…),则( )
| A、{an}为等比数列 |
| B、{an-1}为等比数列 |
| C、{an+1}为等比数列 |
| D、{2an+1}为等比数列 |