将函数y=1+23x-x2-1(x∈[0.23])的图象绕坐标原点逆时针方向旋转角θ.得到曲线C．若对于每一个旋转角θ.曲线AA1=BC=AB=2都是一个函数的图象.则α的最大值为．——青夏教育精英家教网——

-1（x∈[0，2

]）的图象绕坐标原点逆时针方向旋转角θ（0≤θ≤α），得到曲线C．若对于每一个旋转角θ，曲线AA₁=BC=AB=2都是一个函数的图象，则α的最大值为

已知椭圆C的中心在原点，焦点在x轴上，以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形（记为Q）
（1）求椭圆C的方程；
（2）设点P是椭圆C的左准线与x轴的交点，过点P的直线l与椭圆C相交于M、N两点，当线段MN的中点落在正方形Q内（包括边界）时，求直线l的斜率的取值范围．

已知两点M（0，2），N（0，-2），且点P到这两点的距离和等于6．
（1）求动点P的轨迹方程；
（2）若A，B是动点P的轨迹上的两点，且点M分有向线段AB的比为2，求线段AB所在直线的方程．

若角α与角β的终边关于原点成中心对称，则α与β的关系是

图①是一个边长为（m+n）的正方形，小明将图①中的阴影部分拼成图②的形状，由图①和图②能验证的式子是（　　）

A、（m+n）²-（m-n）²=4mn

B、（m+n）²-（m²+n²）=2mn

C、（m-n）²+2mn=m²+n²

D、（m+n）（m-n）=m²-n²

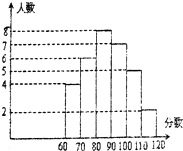某中学部分学生参加市数学竞赛取得了优异成绩，指导老师统计了所有参赛同学的成绩（成绩都为整数，满分120分），并且绘制了“频数分布直方图”（如图）如果90分以上（含90分）获奖，那么该校参赛学生的获奖率为（　　）

对甲、乙两名自行车赛手在相同条件下进行了6次测试，测得他们的最大速度（m/s）的数据如表：

甲	27	38	30	37	35	31
乙	33	29	38	34	28	36

（1）画出茎叶图，并分别求出甲乙两名自行车赛手最大速度的平均数；
（2）分别求出甲乙两名自行车赛手的方差，并判断选谁参加比赛．
（注：方差s²=

）²+…+（x_n-

）²]，其中

为x₁，x₂，…，x_n的平均数）

已知函数f（x）=e^x-e^-x-2x，x∈R
（1）证明f（x）为奇函数，并在R上为增函数；
（2）若关于x的不等式f（x）≤me^x-2x+2m-3在（0，+∞）上恒成立，求实数m的取值范围；
（3）设g（x）=f（2x）-4bf（x），当x＞0时，g（x）＞0，求b的最大值．

已知函数f（x）=lnx+x²-ax，a∈R．
（Ⅰ）当a=3时，求f（x）的单调区间；
（Ⅱ）若x＞1，f（x）＞0，求a的取值范围．

已知f（x）=lg

，且f（x）+f（y）=f（z），则z=

0 204937 204945 204951 204955 204961 204963 204967 204973 204975 204981 204987 204991 204993 204997 205003 205005 205011 205015 205017 205021 205023 205027 205029 205031 205032 205033 205035 205036 205037 205039 205041 205045 205047 205051 205053 205057 205063 205065 205071 205075 205077 205081 205087 205093 205095 205101 205105 205107 205113 205117 205123 205131 266669