题目内容
若角α与角β的终边关于原点成中心对称，则α与β的关系是 ．
考点：终边相同的角
专题：三角函数的求值
分析：由角α与角β的终边关于原点成中心对称，可得α=β+2kπ+π或β=α+2kπ+π（k∈Z）．
解答：
解：∵角α与角β的终边关于原点成中心对称，
α=β+2kπ+π或β=α+2kπ+π．（k∈Z）
故答案为：α=β+2kπ+π或β=α+2kπ+π（k∈Z）．
α=β+2kπ+π或β=α+2kπ+π．（k∈Z）
故答案为：α=β+2kπ+π或β=α+2kπ+π（k∈Z）．
点评：本题考查了终边相同的角直角的关系，属于基础题．
练习册系列答案
相关题目
函数f（x）=x-
在区间（1，+∞）上是增函数，则实数p的取值范围是（ ）
| p |
| x |
| A、（-∞，-1] |
| B、（-∞，1] |
| C、[-1，+∞） |
| D、[1，+∞） |
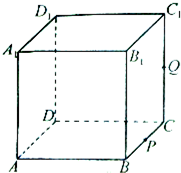如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S．则下列命题正确的是
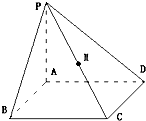如图，四棱锥P-ABCD中，四边形ABCD是矩形，PA⊥平面ABCD，且AP=