题目内容
将函数y=
-1(x∈[0,2
])的图象绕坐标原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线AA1=BC=AB=2都是一个函数的图象,则α的最大值为 .
1+2
|
| 3 |
考点:旋转变换
专题:函数的性质及应用,矩阵和变换
分析:本题可以将曲线方程化简,得到相应的一个圆的方程,得知原函数图象是圆的一部分,通过旋转变换,根据图象特征,得到本题结论.
解答:
解:∵函数y=
-1(x∈[0,2
]),
∴(x-
)2+(y+1)2=4,x∈[0,2
]),y∈[-1,1].
原函数图象是以C(
,-1)为圆心,半径为2的圆的一总分.
过原点O作圆C的切线l,
∵kOC=
=-
,
∴kl=-
=
.
∴直线l的倾斜角为
,
∴旋转直线l与y轴重合时,θ=
.
∴α的最大值为
.
1+2
|
| 3 |
∴(x-
| 3 |
| 3 |
原函数图象是以C(
| 3 |
过原点O作圆C的切线l,
∵kOC=
| -1-0 | ||
|
| ||
| 3 |
∴kl=-
| 1 |
| kOC |
| 3 |
∴直线l的倾斜角为
| π |
| 3 |
∴旋转直线l与y轴重合时,θ=
| π |
| 6 |
∴α的最大值为
| π |
| 6 |
点评:本题考查了曲线的方程,曲线的切线,还考查了函数图象的概念,本题难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数f(x)=(x2-8x+c1)(x2-8x+c2)(x2-8x+c3) (x2-8x+c4),集合M={x|f(x)=0}={x1,x2…,x7}⊆N+,设c1≥c2≥c3≥c4,则c1-c4( )
| A、9 | B、8 | C、7 | D、6 |
若xy≠0,则等式
=-4xy
成立的条件是( )
| 16x2y3 |
| y |
| A、x>0,y>0 |
| B、x>0,y<0 |
| C、x<0,y>0 |
| D、x<0,y<0 |
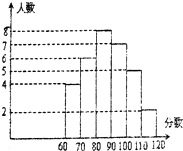 某中学部分学生参加市数学竞赛取得了优异成绩,指导老师统计了所有参赛同学的成绩(成绩都为整数,满分120分),并且绘制了“频数分布直方图”(如图)如果90分以上(含90分)获奖,那么该校参赛学生的获奖率为( )
某中学部分学生参加市数学竞赛取得了优异成绩,指导老师统计了所有参赛同学的成绩(成绩都为整数,满分120分),并且绘制了“频数分布直方图”(如图)如果90分以上(含90分)获奖,那么该校参赛学生的获奖率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
一个几何体的三视图如图所示(单位:m),则该几何体的体积为( )
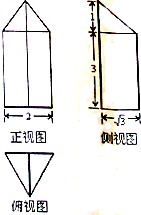

A、2
| ||||
B、4
| ||||
C、
| ||||
D、
|