题目内容
已知两点M(0,2),N(0,-2),且点P到这两点的距离和等于6.
(1)求动点P的轨迹方程;
(2)若A,B是动点P的轨迹上的两点,且点M分有向线段AB的比为2,求线段AB所在直线的方程.
(1)求动点P的轨迹方程;
(2)若A,B是动点P的轨迹上的两点,且点M分有向线段AB的比为2,求线段AB所在直线的方程.
考点:轨迹方程,直线的一般式方程
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)由题意得,|MN|=4,|PM|+|PN|=6>4,设P(x,y),则由椭圆的定义可得,P的轨迹为椭圆,根据题意的标准方程即可求得;
(2)可设直线AB:y=kx+2,A(x1,y1),B(x2,y2),联立直线方程和椭圆方程,消去y,运用韦达定理和向量的坐标公式,解关于x1,x2,k的方程,即可得到k,进而得到所求直线方程.
(2)可设直线AB:y=kx+2,A(x1,y1),B(x2,y2),联立直线方程和椭圆方程,消去y,运用韦达定理和向量的坐标公式,解关于x1,x2,k的方程,即可得到k,进而得到所求直线方程.
解答:
解:(1)由题意得,|MN|=4,|PM|+|PN|=6>4,
设P(x,y),则由椭圆的定义可得,P的轨迹为椭圆,
且焦点为M,N,则2a=6,即a=3,又c=2,
则b2=a2-c2=5,
故动点P的轨迹方程为:
+
=1;
(2)可设直线AB:y=kx+2,A(x1,y1),B(x2,y2),
由
消去y得,(9+5k2)x2+20kx-25=0,
则x1+x2=-
,①x1x2=
,②
又
=2
,即有-x1=2x2,③
③分别代入①、②,可得
=
,
解得,k=±
.
则直线AB的方程为:y=±
x+2.
设P(x,y),则由椭圆的定义可得,P的轨迹为椭圆,
且焦点为M,N,则2a=6,即a=3,又c=2,
则b2=a2-c2=5,
故动点P的轨迹方程为:
| y2 |
| 9 |
| x2 |
| 5 |
(2)可设直线AB:y=kx+2,A(x1,y1),B(x2,y2),
由
|
则x1+x2=-
| 20k |
| 9+5k2 |
| -25 |
| 9+5k2 |
又
| AM |
| MB |
③分别代入①、②,可得
| 2×400k2 |
| (9+5k2)2 |
| 25 |
| 9+5k2 |
解得,k=±
| ||
| 3 |
则直线AB的方程为:y=±
| ||
| 3 |
点评:本题考查椭圆的定义、性质和方程,考查联立直线方程和椭圆方程,消去未知数,运用韦达定理,及向量的坐标解决问题,考查运算能力,属于中档题.

练习册系列答案
相关题目
在锐角△ABC中,则有( )
| A、cosA>sinB且cosB>sinA |
| B、cosA<sinB且cosB<sinA |
| C、cosA>sinB且cosB<sinA |
| D、cosA<sinB且cosB>sinA |
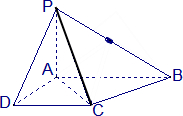 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=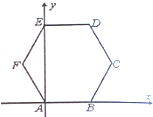 如图,正六边形ABCDEF的边长为2,分别以AB,AE所在直线为x,y轴建立直角边坐标系,用斜二测画法得到水平放置的正六边形ABCDEF的直观图A′B′C′D′E′F′,则六边形A′B′C′D′E′F′的面积为
如图,正六边形ABCDEF的边长为2,分别以AB,AE所在直线为x,y轴建立直角边坐标系,用斜二测画法得到水平放置的正六边形ABCDEF的直观图A′B′C′D′E′F′,则六边形A′B′C′D′E′F′的面积为