题目内容
已知f(x)=lg
,且f(x)+f(y)=f(z),则z= .
| 1-x |
| 1+x |
考点:对数的运算性质
专题:函数的性质及应用
分析:由条件求得f(x)+f(y)=lg
=f(z)=lg
,从而求得z的值.
1-
| ||
1-
|
| 1-z |
| 1+z |
解答:
解:∵f(x)=lg
,∴f(x)+f(y)=lg
+lg
=lg
=lg
=lg
=f(z)=lg
,
∴z=
,
故答案为:
.
| 1-x |
| 1+x |
| 1-x |
| 1+x |
| 1-y |
| 1+y |
| 1-x-y+xy |
| 1+x+y+xy |
| 1+xy-(x+y) |
| 1+xy+(x+y) |
1-
| ||
1-
|
| 1-z |
| 1+z |
∴z=
| x+y |
| 1+xy |
故答案为:
| x+y |
| 1+xy |
点评:本题主要考查对数的运算性质的应用,式子的变形是解题的关键,属于基础题.

练习册系列答案
相关题目
若函数y=
x3-x2+1(0<x<2)的图象上任意点处切线的倾斜角为α,则α的最小值是( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在锐角△ABC中,则有( )
| A、cosA>sinB且cosB>sinA |
| B、cosA<sinB且cosB<sinA |
| C、cosA>sinB且cosB<sinA |
| D、cosA<sinB且cosB>sinA |
 图①是一个边长为(m+n)的正方形,小明将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )
图①是一个边长为(m+n)的正方形,小明将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )| A、(m+n)2-(m-n)2=4mn |
| B、(m+n)2-(m2+n2)=2mn |
| C、(m-n)2+2mn=m2+n2 |
| D、(m+n)(m-n)=m2-n2 |
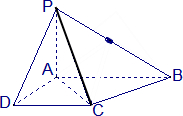 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=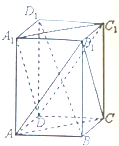 如图,在长方体ABCD-A1B1C1D1中,BB1=BC.
如图,在长方体ABCD-A1B1C1D1中,BB1=BC.