题目内容
 图①是一个边长为(m+n)的正方形,小明将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )
图①是一个边长为(m+n)的正方形,小明将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )| A、(m+n)2-(m-n)2=4mn |
| B、(m+n)2-(m2+n2)=2mn |
| C、(m-n)2+2mn=m2+n2 |
| D、(m+n)(m-n)=m2-n2 |
考点:基本不等式
专题:函数的性质及应用
分析:本题可以根据两个图形变化前后的面积相等,得到本题结论.
解答:
解:如图①,图中阴影部分的面积可表示为:
S阴=S大正方形-S小正方形
大正方形的面积为:(m+n)2,
小正方形的边长为:
,
∴小形的面积为:m2+n2,
∴S阴=(m+n)2-(m2+n2).
如图②,图中面积为4个直角三角形,
S=4×
mn=2mn.
∴(m+n)2-(m2+n2)=2mn,
故答案为:B.
S阴=S大正方形-S小正方形
大正方形的面积为:(m+n)2,
小正方形的边长为:
| m2+n2 |
∴小形的面积为:m2+n2,
∴S阴=(m+n)2-(m2+n2).
如图②,图中面积为4个直角三角形,
S=4×
| 1 |
| 2 |
∴(m+n)2-(m2+n2)=2mn,
故答案为:B.
点评:本题考查了构造法研究相等关系,本题难度不大,属于基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
执行如图的程序框图,若输入的x∈[0,1],则输出的x的范围是( )


| A、[1,3] |
| B、[3,7] |
| C、[7,15] |
| D、[15,31] |
设M(x0,y0)为抛物线C:y=
x2上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是( )
| 1 |
| 8 |
| A、(2,+∞) | ||
| B、[0,2] | ||
C、(0,
| ||
D、(
|
如图所示,甲、乙、丙是三个空间立体图形的三视图,甲、乙、丙对应的标号正确的是( )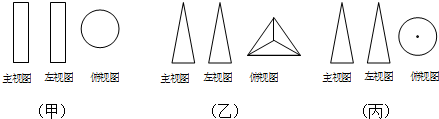
①长方体 ②圆锥 ③三棱锥 ④圆柱.

①长方体 ②圆锥 ③三棱锥 ④圆柱.
| A、③②④ | B、②①③ |
| C、①②③ | D、④③② |
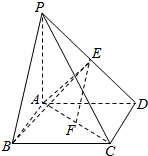 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E,F分别为PA、AC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E,F分别为PA、AC的中点.