已知四面体P-ABC中,PA=4,AC=2
,PB=PC=2
,PA⊥平面PBC,则四面体P-ABC的内切球半径与外接球半径的比( )
| 7 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 在刚刚结束的校运会中,学校要求高一年级全体在篮球场观看比赛,如图所示,某同学为了拍摄下本班同学100m短跑的全过程,希望拍摄点P与100米的起点A,终点B的张角最大,现做如下数学模型:记百米跑道为4个单位(每单位25米),终点B离观赛区直线l距离为1单位,每个班的间距为1单位,如图所示,问该同学最好到哪个班所在的区域拍摄( )
在刚刚结束的校运会中,学校要求高一年级全体在篮球场观看比赛,如图所示,某同学为了拍摄下本班同学100m短跑的全过程,希望拍摄点P与100米的起点A,终点B的张角最大,现做如下数学模型:记百米跑道为4个单位(每单位25米),终点B离观赛区直线l距离为1单位,每个班的间距为1单位,如图所示,问该同学最好到哪个班所在的区域拍摄( )| A、12班 | B、11班 |
| C、10班 | D、9班 |
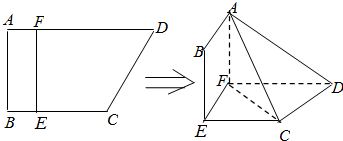
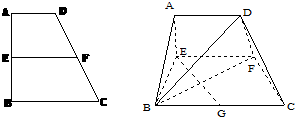 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=