题目内容
已知正数a,b满足a+b+
+
=10,则a+b的取值范围是 .
| 1 |
| a |
| 9 |
| b |
考点:基本不等式
专题:不等式
分析:在a+b+
+
=10的两边同乘以(a+b),展开后求a+b的取值范围.
| 1 |
| a |
| 9 |
| b |
解答:
解:∵a+b+
+
=10,
∴(a+b)(a+b+
+
)=10(a+b),
∴(a+b)2+
+
=(a+b)2+10+
+
=10(a+b),
∴(a+b)2+10+2
≤10(a+b)
∴(a+b)2-10(a+b)+8≤0,
解得2≤a+b≤8.
故答案为:[2,8].
| 1 |
| a |
| 9 |
| b |
∴(a+b)(a+b+
| 1 |
| a |
| 9 |
| b |
∴(a+b)2+
| a+b |
| a |
| 9(a+b) |
| b |
| b |
| a |
| 9a |
| b |
∴(a+b)2+10+2
|
∴(a+b)2-10(a+b)+8≤0,
解得2≤a+b≤8.
故答案为:[2,8].
点评:本题主要考查基本不等式的应用,技巧性较大.

练习册系列答案
相关题目
已知四面体P-ABC中,PA=4,AC=2
,PB=PC=2
,PA⊥平面PBC,则四面体P-ABC的内切球半径与外接球半径的比( )
| 7 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在三棱锥P-ABC中,O是底面正三角形ABC的中心,Q为棱PA上的一点,PA=1,若QO∥平面PBC,则PQ=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
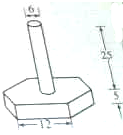 如图是一种机器零件,零件下面是六棱柱(底面是正 六边形,侧面是全等的矩形)形.上面是圆柱(尺寸如图,单位:mm),电镀这种零件需要用锌,已知每平方米用锌0.11kg,问电镀10000个零件需锌多少千克(结果精确到0.01kg).
如图是一种机器零件,零件下面是六棱柱(底面是正 六边形,侧面是全等的矩形)形.上面是圆柱(尺寸如图,单位:mm),电镀这种零件需要用锌,已知每平方米用锌0.11kg,问电镀10000个零件需锌多少千克(结果精确到0.01kg).