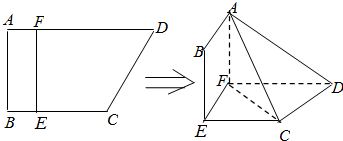
题目内容
(1)如图1,在四面体ABCD中,平行于AB,CD的平面β截四面体所得截面为EFGH.

(ⅰ)若AB=a,CD=b (a>b),求截面EFGH的周长的范围.
(ⅱ)如果AB与CD所成角为θ,AB=a,CD=b是定值,当E在AC何处时?截面EFGH的面积最大,最大值是多少?
(2)如图2,若点M为四面体ABCD底面△BCD的重心,任意作一平行于底面的截面分别与侧棱AB,AC,AD交于B1,C1,D1与AM交于点M1,试探求:
+
+
=x
中x的值,并证明.

(ⅰ)若AB=a,CD=b (a>b),求截面EFGH的周长的范围.
(ⅱ)如果AB与CD所成角为θ,AB=a,CD=b是定值,当E在AC何处时?截面EFGH的面积最大,最大值是多少?
(2)如图2,若点M为四面体ABCD底面△BCD的重心,任意作一平行于底面的截面分别与侧棱AB,AC,AD交于B1,C1,D1与AM交于点M1,试探求:
| AB |
| AB1 |
| AC |
| AC1 |
| AD |
| AD1 |
| AM |
| AM1 |
考点:平面的基本性质及推论,基本不等式在最值问题中的应用
专题:综合题,空间位置关系与距离
分析:(1)(ⅰ)利用线面平行的判定与性质,证出EF∥GH且EH∥FG,从而得到四边形EGFH的两组对边分别平行,即四边形EFGH为平行四边形.
(ⅱ)根据线面平行的性质定理,容易得到AB∥HG,同理可得AB∥EF,所以得到HG∥EF,同理可得到截面EFGH的另一组对边EH∥FG,这样便得到截面EFGH的两组对边都平行,即得到截面EFGH是平行四边形;
(2)利用平面与平面平行的性质,即可得出结论.
(ⅱ)根据线面平行的性质定理,容易得到AB∥HG,同理可得AB∥EF,所以得到HG∥EF,同理可得到截面EFGH的另一组对边EH∥FG,这样便得到截面EFGH的两组对边都平行,即得到截面EFGH是平行四边形;
(2)利用平面与平面平行的性质,即可得出结论.
解答:
(1)(ⅰ)证明:∵AB∥平面EFGH,AB?平面CAB,平面CAB∩平面EFGH=EF
∴AB∥EF.
同理可得BA∥GH,可得EF∥GH,同理得到GF∥HE,
∴四边形EFGH为平行四边形.
且AB=a,CD=b (a>b),∴
=
①,
=
②,
则①+②得,
+
=1,
∴EH=b-
EF,
∴四边形EFGH的周长=2(EH+EF)=2(b+
EF),
∵0<EF<a,∴四边形EFGH的周长为(2b,2a);
(ⅱ)∵BA与DC所成角为θ,
∴平行四边形EFGH中∠EFG=θ或180°-θ,
∵EFGH为平行四边形,令
=λ(0<λ<1),
∵
=
,
=
∴EH=(1-λ)b,EF=λa
SEFGH=EF•EH•sinθ=λa(1-λ)bsinθ=λ(1-λ)absinθ
∴当λ=
时,即E为AC中点时,截面EFGH面积最大,最大值为
absinθ;
(2)当截面无限接近底面时,可得x=3,证明如下:
由题意,任意作一平行于底面的截面分别与侧棱AB,AC,AD交于B1,C1,D1与AM交于点M1,
∴AB∥A1B1,BC∥B1C1,AC∥A1C1,
∴
=
,
=
,
=
,
∴
+
+
=3•
.
∴AB∥EF.
同理可得BA∥GH,可得EF∥GH,同理得到GF∥HE,
∴四边形EFGH为平行四边形.
且AB=a,CD=b (a>b),∴
| EH |
| b |
| AE |
| AC |
| EF |
| a |
| CE |
| AC |
则①+②得,
| EH |
| b |
| EF |
| a |
∴EH=b-
| b |
| a |
∴四边形EFGH的周长=2(EH+EF)=2(b+
| a-b |
| a |
∵0<EF<a,∴四边形EFGH的周长为(2b,2a);
(ⅱ)∵BA与DC所成角为θ,
∴平行四边形EFGH中∠EFG=θ或180°-θ,
∵EFGH为平行四边形,令
| CE |
| CA |
∵
| EH |
| b |
| AE |
| AC |
| EF |
| a |
| CE |
| AC |
∴EH=(1-λ)b,EF=λa
SEFGH=EF•EH•sinθ=λa(1-λ)bsinθ=λ(1-λ)absinθ
∴当λ=
| 1 |
| 2 |
| 1 |
| 4 |
(2)当截面无限接近底面时,可得x=3,证明如下:
由题意,任意作一平行于底面的截面分别与侧棱AB,AC,AD交于B1,C1,D1与AM交于点M1,
∴AB∥A1B1,BC∥B1C1,AC∥A1C1,
∴
| AB |
| AB1 |
| AM |
| AM1 |
| AC |
| AC1 |
| AM |
| AM1 |
| AD |
| AD1 |
| AM |
| AM1 |
∴
| AB |
| AB1 |
| AC |
| AC1 |
| AD |
| AD1 |
| AM |
| AM1 |
点评:考查线面垂直的性质,线面平行的性质定理,以及平行线分线段成比例,属于中档题.

练习册系列答案
相关题目
函数f(x)=ax-
(a>0,a≠1)的图象可能是( )
| 1 |
| a |
A、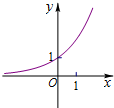 |
B、 |
C、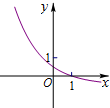 |
D、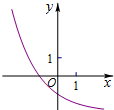 |
如图,AB是⊙O的直径,点C,D是半圆弧AB上的两个三等分点,
=
,
=
,则
=( )
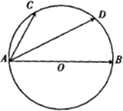
| AB |
| a |
| AC |
| b |
| AD |

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|