Question

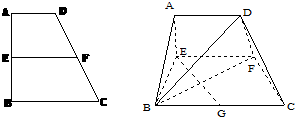已知梯形ABCD中，AD∥BC，∠ABC=∠BAD=

π

2

，AB=BC=2AD=4，E、F分别是AB、CD上的点，EF∥BC，AE=2，G是BC的中点．如图，沿EF将梯形ABCD翻折，使平面AEFD⊥平面EBCF．
（Ⅰ）求证：BD⊥EG；
（Ⅱ）求二面角D-BF-C的余弦值．

Answer 1

考点：二面角的平面角及求法,空间中直线与直线之间的位置关系

专题：综合题,空间位置关系与距离,空间角

分析：（Ⅰ）以E为原点，EB为x轴，EF为y轴，EA为z轴，建立空间直角坐标系，欲证BD⊥EG，只需证

BD

•

EG

=0即可；
（Ⅱ）先求出平面DEF的法向量，利用两平面的法向量求出两向量的夹角的余弦值，从而得到二面角D-BF-C的余弦值．

解答： 解：（Ⅰ）∵平面AEFD⊥平面EBCF，EF∥AD，∠AEF=

π

2

，
∴AE⊥EF，∴AE⊥平面EBCF，AE⊥EF，AE⊥BE，
又BE⊥EF，故可如图建立空间坐标系E-xyz．
∵EA=2，∴EB=2，
又∵G为BC的中点，BC=4，
∴BG=2．则A（0，0，2），B（2，0，0），G（2，2，0），D（0，2，2），E（0，0，0），
∴

BD

=（-2，2，2），

EG

=（2，2，0），
∴

BD

•

EG

=（-2，2，2）•（2，2，0）=0，
∴BD⊥EG．…（4分）
（Ⅱ）设平面DEF的法向量为

n1

=（x，y，z），
∵AE=2，B（2，0，0），D（0，2，2），F（0，3，0），∴

BF

=(-2，3，0)，…（6分）

BD

=（-2，2，2），则 

n1 • BD =0 n1 • BF =0

，
即

(x，y，z)•(-2，2，2)=0 (x，y，z)•(-2，3，0)=0

，

-2x+2y+2z=0 -2x+3y=0

取x=3，y=2，z=1，∴

n1

=(3，2，1)
∵AE⊥面BCF，∴面BCF一个法向量为

n2

=(0，0，1)，…（8分）
则cos＜

n1

，

n2

＞=

n1 • n2

|n1 || n2|

=

14

14

，
由于所求二面角D-BF-C的平面角为钝角，所以此二面角的余弦值为-

14

14

．…（10分）

点评：立几中对空间的线线、线面、面面关系的考查是主线，在理科生中对空间向量的要求也是课标要求．