已知等差数列{an}的前n项和为Sn,若Sn=2,S2n=14,则S4n=( )
| A、68 | B、30 | C、26 | D、16 |
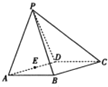 如图,四棱锥P-BCDE中,四边形ABCD为菱形,且∠DAB=60°,△PAD为对边三角形,平面PAD⊥平面ABCD,AB=2,E为AD的中点.
如图,四棱锥P-BCDE中,四边形ABCD为菱形,且∠DAB=60°,△PAD为对边三角形,平面PAD⊥平面ABCD,AB=2,E为AD的中点.(1)求证:AD⊥PB;
(2)求点E到平面PBC的距离.
| A、68 | B、30 | C、26 | D、16 |
 如图,四棱锥P-BCDE中,四边形ABCD为菱形,且∠DAB=60°,△PAD为对边三角形,平面PAD⊥平面ABCD,AB=2,E为AD的中点.
如图,四棱锥P-BCDE中,四边形ABCD为菱形,且∠DAB=60°,△PAD为对边三角形,平面PAD⊥平面ABCD,AB=2,E为AD的中点.