题目内容
已知双曲线
-
=1(b>0)的左、右焦点分别是F1、F2,其中一条渐近线方程为y=x,点P(x0,y0)在双曲线,求
•
的范围.
| x2 |
| 2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
考点:双曲线的简单性质
专题:计算题,平面向量及应用,圆锥曲线的定义、性质与方程
分析:由双曲线方程写出渐近线,由已知可得b,再由数量积的坐标公式,结合点P在双曲线上,得到所求数量积为2x02-6,再由双曲线的范围,即可得到范围.
解答:
解:双曲线
-
=1(b>0)的渐近线方程为:y=±
x,
由于其中一条渐近线方程为y=x,则b=
,
即有双曲线方程为:x2-y2=2.
即有左、右焦点分别是F1(-2,0),F2(2,0),
则
•
=(-2-x0,-y0)•(2-x0,-y0)=x02+y02-4
又点P(x0,y0)在双曲线上,即有x02-y02=2,
即y02=x02-2,
即有
•
=2x02-6,
由双曲线的性质,可得x02≥2,
则有
•
≥4-6=-2.
故所求范围是[-2,+∞).
| x2 |
| 2 |
| y2 |
| b2 |
| b | ||
|
由于其中一条渐近线方程为y=x,则b=
| 2 |
即有双曲线方程为:x2-y2=2.
即有左、右焦点分别是F1(-2,0),F2(2,0),
则
| PF1 |
| PF2 |
又点P(x0,y0)在双曲线上,即有x02-y02=2,
即y02=x02-2,
即有
| PF1 |
| PF2 |
由双曲线的性质,可得x02≥2,
则有
| PF1 |
| PF2 |
故所求范围是[-2,+∞).
点评:本题考查双曲线的方程和性质,考查平面向量的数量积的坐标表示,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若椭圆2kx2+ky2=1的一个焦点坐标是(0,4),则实数k的值为( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
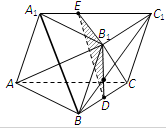 如图,在三棱柱ABC-A1B1C1中,D是BC的中点.
如图,在三棱柱ABC-A1B1C1中,D是BC的中点.