题目内容
在四棱锥S-ABCD中,平面SAB⊥平面SAD,侧面SAB是边长为2
的等边三角形,底面ABCD是矩形,且BC=4,则该四棱锥外接球的表面积等于 .
| 3 |
考点:平面与平面垂直的性质,球内接多面体
专题:空间位置关系与距离
分析:依题意,设AB的中点为E,作图如下,利用面面垂直的性质与线面垂直的判定定理可证得SE⊥底面ABCD,设该四棱锥外接球的球心为O,半径为R,O到底面的距离为h,则r2+h2=R2,即7+h2=R2=4+(3-h)2,可求得h与R,从而可得该四棱锥外接球的表面积.
解答:
解:∵平面SAB⊥平面SAD,平面SAB∩平面SAD=SA,侧面SAB是边长为2
的等边三角形,设AB的中点为E,SA的中点为F,
则BF⊥SA,∴BF⊥平面SAD,∴BF⊥AD,底面ABCD是矩形,∴AD⊥平面SAB,SE?平面SAB,
∴AD⊥SE,又SE⊥AB,AB∩AD=A,
∴SE⊥底面ABCD,作图如下:

∵SAB是边长为2
的等边三角形,
∴SE=2
sin60°=2
×
=3.
又底面ABCD是矩形,且BC=4,
∴矩形ABCD的对角线长为
=2
,
∴矩形ABCD的外接圆的半径为r=
.
设该四棱锥外接球的球心为O,半径为R,O到底面的距离为h,
则r2+h2=R2,即7+h2=R2,又R2=22+(SE-h)2=4+(3-h)2,
∴7+h2=4+(3-h)2,
∴h=1.
∴R2=7+h2=8,R=2
,
∴该四棱锥外接球的表面积S球=4π×(2
)2=32π.
| 3 |
则BF⊥SA,∴BF⊥平面SAD,∴BF⊥AD,底面ABCD是矩形,∴AD⊥平面SAB,SE?平面SAB,
∴AD⊥SE,又SE⊥AB,AB∩AD=A,
∴SE⊥底面ABCD,作图如下:

∵SAB是边长为2
| 3 |
∴SE=2
| 3 |
| 3 |
| ||
| 2 |
又底面ABCD是矩形,且BC=4,
∴矩形ABCD的对角线长为
42+(2
|
| 7 |
∴矩形ABCD的外接圆的半径为r=
| 7 |
设该四棱锥外接球的球心为O,半径为R,O到底面的距离为h,
则r2+h2=R2,即7+h2=R2,又R2=22+(SE-h)2=4+(3-h)2,
∴7+h2=4+(3-h)2,
∴h=1.
∴R2=7+h2=8,R=2
| 2 |
∴该四棱锥外接球的表面积S球=4π×(2
| 2 |
点评:本题考查面面垂直的性质与线面垂直的判定定理,着重考查球内接多面体中球的半径的运算,属于难题.

练习册系列答案
相关题目
已知抛物线y2=4x,焦点为P,平面上一定点A(m,0),满足
=2
,过A作直线l,过原点作l的垂线,垂足为Q,则Q的轨迹方程为( )
| OA |
| PA |
| A、y=2x(x≠0) |
| B、x2+y2=1(x≠0) |
| C、(x-1)2+y2=1(y≠0) |
| D、x2-2xy+y2=0(x≠0) |
若|cos(
-α)|=sin(π+α),则角α的取值范围是( )
| 3π |
| 2 |
| A、[2kπ-π,2kπ](k∈Z) | ||||
| B、[2kπ,2kπ+π](k∈Z) | ||||
C、[2kπ-
| ||||
D、[2kπ+
|
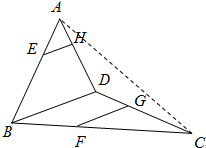 如图,空间四边形ABCD中,E、H为AB、AD的中点,G、F为BC、CD上的点,且
如图,空间四边形ABCD中,E、H为AB、AD的中点,G、F为BC、CD上的点,且