题目内容
若点(x,y)在椭圆4x2+y2=4上,则
的最大值为 ,最小值为 .
| y-1 |
| x-2 |
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:把
的最值转化为求过点(2,1)的直线与椭圆4x2+y2=4的切线问题,设出过点(2,1)的直线方程,和椭圆方程联立,利用判别式等于0得答案.
| y-1 |
| x-2 |
解答:
解:椭圆4x2+y2=4的图象如图,
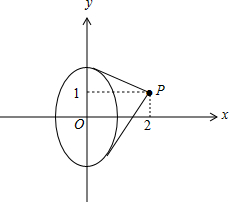
设过P(2,1)的直线方程为y-1=k(x-2),
联立
,得(4+k2)x2-(4k2-2k)x+4k2-4k-3=0.
由△=(4k2-2k)2-4(4+k2)(4k2-4k-3)=0,
解得:k1=
,k2=
.
∴
的最大值为
,最小值为
.
故答案为:
;
.

设过P(2,1)的直线方程为y-1=k(x-2),
联立
|
由△=(4k2-2k)2-4(4+k2)(4k2-4k-3)=0,
解得:k1=
2-
| ||
| 3 |
2+
| ||
| 3 |
∴
| y-1 |
| x-2 |
2+
| ||
| 3 |
2-
| ||
| 3 |
故答案为:
2+
| ||
| 3 |
2-
| ||
| 3 |
点评:本题考查了直线与圆锥曲线的关系,考查了数学转化思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
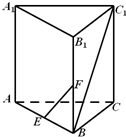 如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC,∠ABC=90°,点E,F分别是棱AB,BB1的中点,则直线EF和BC1所成的角是( )
如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC,∠ABC=90°,点E,F分别是棱AB,BB1的中点,则直线EF和BC1所成的角是( )| A、45° | B、135° |
| C、60° | D、120° |
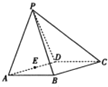 如图,四棱锥P-BCDE中,四边形ABCD为菱形,且∠DAB=60°,△PAD为对边三角形,平面PAD⊥平面ABCD,AB=2,E为AD的中点.
如图,四棱锥P-BCDE中,四边形ABCD为菱形,且∠DAB=60°,△PAD为对边三角形,平面PAD⊥平面ABCD,AB=2,E为AD的中点.