题目内容
已知等差数列{an}的前n项和为Sn，若Sn=2，S2n=14，则S4n=（ ）
| A、68 | B、30 | C、26 | D、16 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：由等差数列的性质可得出Sn，S2n-Sn，S3n-S2n，S4n-S3n成等差数列，再结合根据题设即可求出S4n的值．
解答：
解：∵等差数列{an}
∴Sn，S2n-Sn，S3n-S2n，S4n-S3n成等差数列，
又Sn=2，S2n=14，
Sn=2，S2n-Sn=12，S3n-S2n=22，S4n-S3n=32，
∴S4n=68．
故选A．
∴Sn，S2n-Sn，S3n-S2n，S4n-S3n成等差数列，
又Sn=2，S2n=14，
Sn=2，S2n-Sn=12，S3n-S2n=22，S4n-S3n=32，
∴S4n=68．
故选A．
点评：本题考查等差数列的性质，牢固记忆性质是解答本题的关键，本题属于基本题型，计算题．
练习册系列答案
相关题目
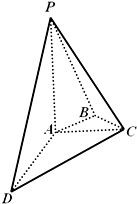如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1．
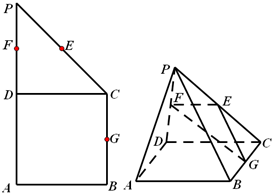如图，在直角梯形ABCP中，BC∥AP，AB⊥BC，CD⊥AP，AD=CD=PD，E，F，G分别为线段PC，PD，BC的中点，现将△PDC折起，使点P∉平面ABCD．求证：PA∥面EFG．
如图，已知△ABC的面积是1，BD=2DC，CE=3EA，AD与BE相交于点F，请写出这4部分的面积各是多少？