 设抛物线y2=4x的焦点为F,过点(
设抛物线y2=4x的焦点为F,过点(| 1 |
| 2 |
(Ⅰ)求点M的轨迹方程;
(Ⅱ)设直线PQ的斜率为k,用k表示△APQ的面积.
双曲线的焦点在y轴上,且它的一个焦点在直线5x-2y+20=0上,两焦点关于原点对称.
=
,则此双曲线的方程是( )
| c |
| a |
| 5 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某几何体的立体图如图所示,该几何体的三视图不可能是( )
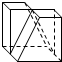

A、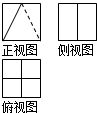 |
B、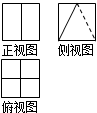 |
C、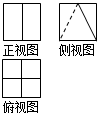 |
D、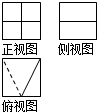 |
 设抛物线y2=4x的焦点为F,过点(
设抛物线y2=4x的焦点为F,过点(| 1 |
| 2 |
| c |
| a |
| 5 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

A、 |
B、 |
C、 |
D、 |