题目内容
在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,若b=1,c=
.求∠C的取值范围.
| ||
| 2 |
考点:余弦定理
专题:计算题,解三角形
分析:由余弦定理知:cos∠C=
+
≥2
=
.即有cos∠C≥cos
,又0<∠C<π,从而由余弦函数的图象可知0<∠C≤
.
| a |
| 2 |
| 1 |
| 8a |
|
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
解答:
解:由余弦定理知:cos∠C=
=
=
=
+
≥2
=
.
∵有cos∠C≥cos
,0<∠C<π,
∴余弦函数的图象可知:0<∠C≤
.
| a2+b2-c2 |
| 2ab |
a2+1-
| ||
| 2a |
a2+
| ||
| 2a |
| a |
| 2 |
| 1 |
| 8a |
|
| 1 |
| 2 |
∵有cos∠C≥cos
| π |
| 3 |
∴余弦函数的图象可知:0<∠C≤
| π |
| 3 |
点评:本题主要考察了余弦定理的应用,属于基本知识的考查.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
若x可以在|x+1|≤3的条件下任意取值,则x是负值的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设A、B为椭圆
+
=1上任意两点,O为坐标原点,则“OA⊥OB”是“O到直线AB的距离为
”的( )
| x2 |
| 16 |
| y2 |
| 9 |
| 12 |
| 5 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
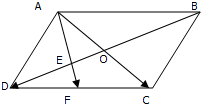 如图所示,已知?ABCD,E是OD的中点,
如图所示,已知?ABCD,E是OD的中点,