设f(x)是定义在R上的不恒为零的函数,且对于任意的a,b∈R满足f(ab)-af(b)=bf(a),f(3)=3,an=
,bn=
,n∈N*.有下列结论:
①f(
)=
;②f(x)为奇函数;③a2=-2;④b2=9.
其中正确的是( )
| f(3n) |
| 3n |
| f(3n) |
| n |
①f(
| 1 |
| 3 |
| 1 |
| 3 |
其中正确的是( )
| A、①②③ | B、③④ | C、①③ | D、②④ |
用a,b表示两条不同的直线,γ表示平面,给出下列命题:
(1)若a∥γ,b∥γ,则a∥b
(2)若a∥b,b∥γ,则a∥γ
(3)若a⊥γ,b∥γ,则a⊥b
(4)若a⊥γ,b⊥γ,则a∥b
其中真命题的序号是( )
(1)若a∥γ,b∥γ,则a∥b
(2)若a∥b,b∥γ,则a∥γ
(3)若a⊥γ,b∥γ,则a⊥b
(4)若a⊥γ,b⊥γ,则a∥b
其中真命题的序号是( )
| A、(1)(4) |
| B、(2)(3) |
| C、(3)(4) |
| D、(1)(2) |
| a |
| b |
| a |
| b |
| A、2 | B、1 | C、0 | D、-2 |
数列{
}的前n项和为Sn,且满足a1=1,an=an-1+n,(n≥2),则Sn等于( )
| an |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
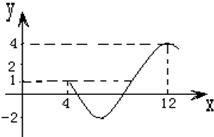 如图为函数f(x)=Asin(ωx+ϕ)+c(A>0,ω>0,0<ϕ<2π)图象的一部分.
如图为函数f(x)=Asin(ωx+ϕ)+c(A>0,ω>0,0<ϕ<2π)图象的一部分.