Question

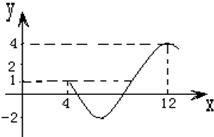如图为函数f（x）=Asin（ωx+ϕ）+c（A＞0，ω＞0，0＜ϕ＜2π）图象的一部分．
（1）求函数f（x）的解析式，并写出f（x）的振幅、周期、初相；
（2）求使得f（x）＞

5

2

的x的集合；
（3）函数f（x）的图象可由函数y=sinx的图象经过怎样的变换而得到？

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,函数y=Asin（ωx+φ）的图象变换

专题：三角函数的图像与性质

分析：（1）首先，根据所给函数图象，确定其振幅A，然后，确定其解析式；
（2）直接结合正弦函数的单调性进行求解；
（3）直接根据平移知识求解．

解答：
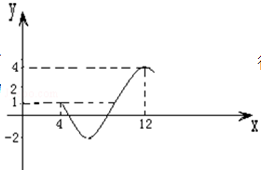
解：（1）由函数图象可知函数的最大值为A+c=4，最小值为-A+c=-2，
∴c=1，A=3，
∵

3

4

T=12-4=8，
∴函数的周期T=

32

3

．
由

2π

ω

=

32

3

得，
ω=

3π

16

，
∴y=3sin（

3π

16

x+ϕ）+1
∵（12，4）在函数图象上，
∴4=3sin（

3π

16

•12+ϕ）+1，即sin（

9π

4

+ϕ）=1，
∴

9π

4

+ϕ=

π

2

+2kπ，k∈Z，得ϕ=-

7π

4

+2kπ，k∈Z，
∵0＜ϕ＜2π，∴ϕ=

π

4

，
∴函数解析式为y=3sin（

3π

16

•x+

π

4

）+1．
（2）∵f（x）＞

5

2

，
结合（1），得
3sin（

3π

16

•x+

π

4

）+1＞

5

2

．
解得x∈(-

4

9

+

32

3

k，

28

9

+

32

3

k)，（k∈z）
∴f（x）＞

5

2

的x的集合：(-

4

9

+

32

3

k，

28

9

+

32

3

k)，（k∈z）
（3）先将函数y=sinx的图象向左平移

π

4

个单位，然后，将所得图象横坐标伸长到原来的

16

3π

倍，然后，再将所得图象纵坐标伸长到原来的3倍，然后，再将所得函数图象上所有各点图象向上平移1个单位，即得所求函数的图象．

点评：本题重点考查了三角函数、三角函数图象与性质等知识，三角函数图象平移是近几年高考的热点也是难点问题，需要引起足够重视．