题目内容
若a,b,c>0,且2a+b+c=4,则t=a(a+b+c)+bc的最大值为 .
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:利用基本不等式,即可得出结论.
解答:
解:∵a,b,c都是正数,2a+b+c=4,
∴t=a(a+b+c)+bc=a2+ab+ac+bc=(a+b)(a+c)≤(
)2=(
)2=22=4,
∴a2+ab+ac+bc的最大值为4,
故答案为:4.
∴t=a(a+b+c)+bc=a2+ab+ac+bc=(a+b)(a+c)≤(
| a+b+a+c |
| 2 |
| 4 |
| 2 |
∴a2+ab+ac+bc的最大值为4,
故答案为:4.
点评:本题考查最值问题,正确因式分解,利用基本不等式是关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
已知直线l1与直线l2:3x+4y-6=0平行且与圆:x2+y2+2y=0相切,则直线l1的方程是( )
| A、3x+4y-1=0 |
| B、3x+4y+1=0或3x+4y-9=0 |
| C、3x+4y+9=0 |
| D、3x+4y-1=0或3x+4y+9=0 |
下列命题中是假命题的是( )
| A、?a>0,f(x)=lnx-a有零点 |
| B、?m∈R,使f(x)=(m-1)•xm2-4m+3是幂函数,且在(0,+∞)上递减 |
| C、?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数 |
| D、若y=f(x)的图象关于某点对称,那么?a,b∈R使得y=f(x-a)+b是奇函数 |
下列命题中,正确的是( )
| A、命题“?x∈R,x2-x≤0”的否定是“?x∈R,x2-x≥0” | ||||
| B、“p∧q为真”是命题“p∨a为真”的必要不充分条件 | ||||
| C、“若am2<bm2,则a<b”的否命题为真 | ||||
D、已知a,b∈R,则“log3a>log3b”是“(
|
 如图,直角△ABC的斜边AB=2
如图,直角△ABC的斜边AB=2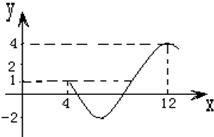 如图为函数f(x)=Asin(ωx+ϕ)+c(A>0,ω>0,0<ϕ<2π)图象的一部分.
如图为函数f(x)=Asin(ωx+ϕ)+c(A>0,ω>0,0<ϕ<2π)图象的一部分.