题目内容
已知关于x的方程
=k在（0，+∞）有且只有两根，记为α、β（α＜β），则βtanβ= ．
| |cosx| |
| x |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：由函数f（x）=|cosx|-kx得到g（x）=|cosx|和函数h（x）=kx，再画出两函数的图象，问题得解．
解答：
解；解：原题等价于方程|cosx|=kx在（0，+∞）恰有两个不同的解，
等价于函数g（x）=|cosx|与函数h（x）=kx的图象在（0，+∞）恰有两个交点（如图），
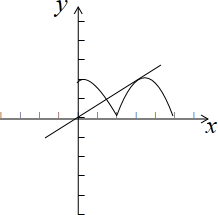
在（
，π）内的交点横坐标为β，且此时直线h（x）=kx与曲线g（x）=|cosx|相切，切点为（β，kβ），
又x∈（
，π）时，g（x）=-cosx，g'（x）=sinx，
故k=g'（β）=sinβ，∴kβ=g（β）=-cosβ．
即cosβ=-βsinβ，
βtanβ=-1
故答案为：-1
等价于函数g（x）=|cosx|与函数h（x）=kx的图象在（0，+∞）恰有两个交点（如图），
在（
| π |
| 2 |
又x∈（
| π |
| 2 |
故k=g'（β）=sinβ，∴kβ=g（β）=-cosβ．
即cosβ=-βsinβ，
βtanβ=-1
故答案为：-1
点评：考查函数零点，导数的应用，解题时可结合图形，难度适中．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
设函数y=f（x）是定义在R上的函数，并且对任意的实数x，y都满足f（x+y）=f（x）•f（y）．当x＞0时，f（x）＞1，f（1）=2．
（1）求f（0）和f（3）的值；
（2）证明f（x）是增函数．
（1）求f（0）和f（3）的值；
（2）证明f（x）是增函数．
已知锐角△ABC中，角A、B、C的对边长分别为a、b、c，向量
=（cosC+sinC，1），
=（cosC-sinC，
），且
⊥
．
（1）求角C的大小；
（2）若边c=2，求△ABC面积的最大值．
| m |
| n |
| 1 |
| 2 |
| m |
| n |
（1）求角C的大小；
（2）若边c=2，求△ABC面积的最大值．
已知集合A={（x，y）|y=log2x}，B={（x，y）|y=2x}，则A∩B=（ ）
| A、（0，+∞） | B、{1，2} |
| C、{（1，2）} | D、∅ |
