题目内容
| a |
| b |
| a |
| b |
| A、2 | B、1 | C、0 | D、-2 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：直接利用向量的坐标运算，数量积的求法求解即可．
解答：
解：
=（1，3），
=（-1，1），
则
•
=1×（-1）+3×1=2．
故选：A．
| a |
| b |
则
| a |
| b |
故选：A．
点评：本题考查向量的数量积的求法，基本知识的考查．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知定义在R上的函数f（x）满足下列三个条件：
①对任意的x∈R，都有f（x+4）=f（x）；
②对任意的0≤x1＜x2≤2，都有f（x1）＜f（x2）；
③y=f（x+2）的图象关于y轴对称，
则下列结论中，正确的是（ ）
①对任意的x∈R，都有f（x+4）=f（x）；
②对任意的0≤x1＜x2≤2，都有f（x1）＜f（x2）；
③y=f（x+2）的图象关于y轴对称，
则下列结论中，正确的是（ ）
| A、f（7）＜f（4.5）＜f（6.5） |
| B、f（7）＜f（6.5）＜f（4.5） |
| C、f（4.5）＜f（6.5）＜f（7） |
| D、f（4.5）＜f（7）＜f（6.5） |
不等式x2-3x+2＜0的解集是（ ）
| A、{x|x＜-2或x＞-1} |
| B、{x|x＜1或x＞2} |
| C、{x|1＜x＜2} |
| D、{x|-2＜x-1} |
数列{
}的前n项和为Sn，且满足a1=1，an=an-1+n，（n≥2），则Sn等于（ ）
| an |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
定义在R上的偶函数，f（x）满足：对任意的x1，x2∈（-∞，0]（x1≠x2），有（x1-x2）[f（x2）-f（x1）]＞0，则当n∈N*时，有（ ）
| A、f（-n）＜f（n-1）＜f（n+1） |
| B、f（n-1）＜f（-n）＜f（n+1） |
| C、f（n+1）＜f（-n）＜f（n-1） |
| D、f（n+1）＜f（n-1）＜f（-n） |
设全集为R，函数f（x）=
的定义域为M，函数f（x）=ln（x2-4x）的定义域为N，则M∩N=（ ）
| 4-x2 |
| A、[-2，0） |
| B、（-∞，-2] |
| C、（4，+∞） |
| D、（-∞，0]∪（4，+∞） |
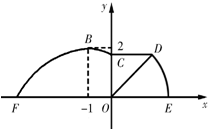如图，某市准备在道路EF的一侧修建一条运动比赛道，赛道的前一部分为曲线段FBC．该曲线段是函数y=Asin（ωx+