已知x，y的取值如下表所示：

x	2	3	4
y	5	4	6

如果x，y呈线性相关，且线性回归方程为

y

=

1

2

x+a，则当x=7时，预测y的值为．

等式1+2+3+…+n=

n(n+1)

2

证明过程如下：
①当n=1时，左边=1，右边=1等式成立；
②假设当n=k时等式成立，即1+2+3+…+k=

k(k+1)

2

，那么当n=k+1时，1+2+3+…+k+（k+1）=

k(k+1)

2

+(k+1)=

(k+1)[(k+1)+1]

2

等式也成立，故原等式成立，以上证明方法是（　　）

已知各项均为正数的数列{a_n}的前n项和为S_n，且4S_n=a_n²+2a_n，设数列{

1

an2

}的前n项和为T_n，求证：T_n＞

5

32

．

已知数列{a_n}中，a₁=1，a_n+1=2a_n+3．求a_n．

如果f（tanx）=sin²x-5sinxcosx，那么f（2）=．

（1）证明：A+B+C=nπ（A，B，C≠kπ+

π

2

，k∈Z，n∈Z）的充要条件是tanA+tanB+tanC=tanAtanBtanC；
（2）利用（1）计算

tan20°+tan40°+tan120°

tan20°tan40°

．

已知集合M={x|x²-2x≤0}，N={x|

3+x

1-x

≤0}，U=R，则图中阴影部分表示的集合是（　　）

设椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的左、右焦点分别为F₁．F₂．A是椭圆上的一点，AF₂⊥F₁F₂，原点O到直线AF₁的距离为

1

3

|OF₁|；
（1）求椭圆的离心率；
（2）若左焦点F₁（-1，0）设过点F₁且不与坐标轴垂直的直线交椭圆于B，C两点，线段BC的垂直平分线与x轴交于G，求点G横坐标的取值范围．

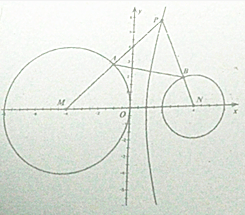已知圆M：x²+8x+y²=0和圆N：x²-8x+y²+12=0，点P（x₀，y₀）（y₀≠0），曲线C：x²-

y2

15

=1右支上的动点，线段PM、PN分别交圆M于A，交圆N于B．
（1）证明：△PAB是等腰三角形；
（2）记△PAB、△PMN的面积分别为S₁、S₂，求

S2

S1

的取值范围．
（3）记点A处圆M的切线为l₁，点B处圆N的切线为l₂，求l₁和l₂交点Q的轨迹方程．

已知函数f（x）

|lgx|，x＞0 1-x2，x≤0

，则方程f（2x²+x）=a（a＞0）的根不可能为（　　）