题目内容
(1)证明:A+B+C=nπ(A,B,C≠kπ+
,k∈Z,n∈Z)的充要条件是tanA+tanB+tanC=tanAtanBtanC;
(2)利用(1)计算
.
| π |
| 2 |
(2)利用(1)计算
| tan20°+tan40°+tan120° |
| tan20°tan40° |
考点:两角和与差的正切函数
专题:三角函数的求值
分析:(1)必要性:若A+B+C=nπ,则A+B=nπ-C,依题意,利用两角和的正切,变形整理,即可证得tanA+tanB+tanC=tanAtanBtanC;
充分性:若tanA+tanB+tanC=tanAtanBtanC,变形后有tanA+tanB=(1-tanAtanB)tanC,逆用两角和的正切,变形整理可得tan(A+B)=tan(-C),继而可得A+B+C=nπ(n∈Z);
(2)观察可知,20°+40°+120°=180°,利用(1)的结论,易求
的值.
充分性:若tanA+tanB+tanC=tanAtanBtanC,变形后有tanA+tanB=(1-tanAtanB)tanC,逆用两角和的正切,变形整理可得tan(A+B)=tan(-C),继而可得A+B+C=nπ(n∈Z);
(2)观察可知,20°+40°+120°=180°,利用(1)的结论,易求
| tan20°+tan40°+tan120° |
| tan20°tan40° |
解答:
(1)证明:必要性:若A+B+C=nπ,则A+B=nπ-C,又A,B,C≠kπ+
,k∈Z,n∈Z,
∴tan(A+B)=tan(nπ-C),
∴
=-tanC,
∴tanA+tanB=-tanC+tanAtanBtanC,
∴tanA+tanB+tanC=tanAtanBtanC;
充分性:若tanA+tanB+tanC=tanAtanBtanC,
则tanA+tanB=-tanC+tanAtanBtanC=(1-tanAtanB)tanC,依题意,1-tanAtanB≠0,
∴
=-tanC,
∴tan(A+B)=tan(-C),
∴A+B=nπ-C,n∈Z,
∴A+B+C=nπ(n∈Z),
∴A+B+C=nπ(A,B,C≠kπ+
,k∈Z,n∈Z)的充要条件是tanA+tanB+tanC=tanAtanBtanC;
(2)解:由∵20°+40°+120°=180°,由(1)知,tan20°+tan40°+tan120°=tan20°tan40°tan120°,
∴
=
=tan120°=-
.
| π |
| 2 |
∴tan(A+B)=tan(nπ-C),
∴
| tanA+tanB |
| 1-tanAtanB |
∴tanA+tanB=-tanC+tanAtanBtanC,
∴tanA+tanB+tanC=tanAtanBtanC;
充分性:若tanA+tanB+tanC=tanAtanBtanC,
则tanA+tanB=-tanC+tanAtanBtanC=(1-tanAtanB)tanC,依题意,1-tanAtanB≠0,
∴
| tanA+tanB |
| 1-tanAtanB |
∴tan(A+B)=tan(-C),
∴A+B=nπ-C,n∈Z,
∴A+B+C=nπ(n∈Z),
∴A+B+C=nπ(A,B,C≠kπ+
| π |
| 2 |
(2)解:由∵20°+40°+120°=180°,由(1)知,tan20°+tan40°+tan120°=tan20°tan40°tan120°,
∴
| tan20°+tan40°+tan120° |
| tan20°tan40° |
| tan20°•tan40°•tan120° |
| tan20°tan40° |
| 3 |
点评:本题考查两角和与差的正切函数,着重考查充分必要性的证明,考查转化思想与推理证明能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

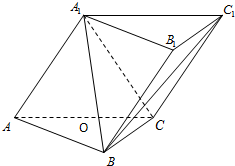 如图,三棱柱ABC-A1B1C1中,侧面AA1CC1垂直于底面ABC,AA1=A1C=AC=2,AB=BC,且AB⊥BC,O为AC中点.
如图,三棱柱ABC-A1B1C1中,侧面AA1CC1垂直于底面ABC,AA1=A1C=AC=2,AB=BC,且AB⊥BC,O为AC中点.