若直线与平面所成的角为0°,则该直线与平面的位置关系是( )
| A、平行 | B、相交 |
| C、直线在平面内 | D、平行或直线在平面内 |
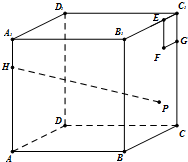 如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA1上,且HA1=1.在侧面BCC1B1内作边长为1的正方形EFGC1,P是侧面BCC1B1内一动点,且点P到平面CDD1C1距离等于线段PF的长.则当点P运动时,|HP|2的最小值是( )
如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA1上,且HA1=1.在侧面BCC1B1内作边长为1的正方形EFGC1,P是侧面BCC1B1内一动点,且点P到平面CDD1C1距离等于线段PF的长.则当点P运动时,|HP|2的最小值是( )| A、21 | B、22 | C、23 | D、25 |
| A、平行 | B、相交 |
| C、直线在平面内 | D、平行或直线在平面内 |
 如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA1上,且HA1=1.在侧面BCC1B1内作边长为1的正方形EFGC1,P是侧面BCC1B1内一动点,且点P到平面CDD1C1距离等于线段PF的长.则当点P运动时,|HP|2的最小值是( )
如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA1上,且HA1=1.在侧面BCC1B1内作边长为1的正方形EFGC1,P是侧面BCC1B1内一动点,且点P到平面CDD1C1距离等于线段PF的长.则当点P运动时,|HP|2的最小值是( )| A、21 | B、22 | C、23 | D、25 |