题目内容
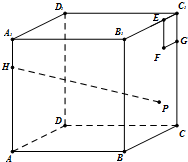如图，已知正方体ABCD-A1B1C1D1棱长为4，点H在棱AA1上，且HA1=1．在侧面BCC1B1内作边长为1的正方形EFGC1，P是侧面BCC1B1内一动点，且点P到平面CDD1C1距离等于线段PF的长．则当点P运动时，|HP|2的最小值是（ ）| A、21 | B、22 | C、23 | D、25 |
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：建立空间直角坐标系，过点H作HM⊥BB′，垂足为M，连接MP，得出HP2=HM2+MP2；
当MP最小时，HP2最小，利用空间直角坐标系求出MP2的最小值即可．
当MP最小时，HP2最小，利用空间直角坐标系求出MP2的最小值即可．
解答：
解：建立空间直角坐标系，如图所示，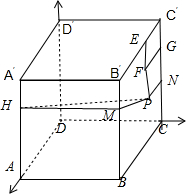
过点H作HM⊥BB′，垂足为M，连接MP，
则HM⊥PM，
∴HP2=HM2+MP2；
当MP最小时，HP2最小，
过P作PN⊥CC′，垂足为N，
设P（x，4，z），则
F（1，4，3），M（4，4，3），N（0，4，z），且4≥x≥0，4≥z≥0；
∵PN=PF，∴
=x，化简得2x-1=（z-3）2；
∴MP2=（x-4）2+（z-3）2=（x-4）2+2x-1=x2-6x+15≥6，
当x=3时，MP2取得最小值，此时HP2=HM2+MP2=42+6=22为最小值．
故选：B．
过点H作HM⊥BB′，垂足为M，连接MP，
则HM⊥PM，
∴HP2=HM2+MP2；
当MP最小时，HP2最小，
过P作PN⊥CC′，垂足为N，
设P（x，4，z），则
F（1，4，3），M（4，4，3），N（0，4，z），且4≥x≥0，4≥z≥0；
∵PN=PF，∴
| (x-1)2+(z-3)2 |
∴MP2=（x-4）2+（z-3）2=（x-4）2+2x-1=x2-6x+15≥6，
当x=3时，MP2取得最小值，此时HP2=HM2+MP2=42+6=22为最小值．
故选：B．
点评：本题考查了空间直角坐标系的应用问题，也考查了空间中的距离的最值问题，是较难的题目．
练习册系列答案
相关题目
设集合A={1，2，3}，B={x|x（x-2）＜0}，则A∩B=（ ）
| A、{1，2，3} |
| B、{2，3} |
| C、{1} |
| D、{1，2} |
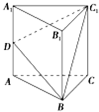如图，在正三棱柱ABC A1B1C1中，D为棱AA1的中点，若截面三角形BC1D是面积为6的直角三角形，则此三棱柱的体积为（ ）A、16
| ||||
B、8
| ||||
C、4
| ||||
D、
|
下列命题中，正确的一个是（ ）
| A、?x0∈R，ln（x02+1）＜0 | ||
| B、?x＞2，x2＞2x | ||
| C、若q是￢p成立的必要不充分条件，则￢q是p成立的充分不必要条件 | ||
D、若x≠kπ（k∈Z），则sin2x+
|