题目内容
已知抛物线y=ax2(a>0)上两个动点A、B(不在原点),满足
⊥OB,若存在定点M,使得
=λ
+μ
且λ+μ=1,则M坐标为 .
| OA |
| OM |
| OA |
| OB |
考点:直线与圆锥曲线的关系
专题:圆锥曲线中的最值与范围问题
分析:由已知得A,B,M三点共线,于是问题转化为动直线过定点,设A(x1,y1),B(x2,y2),则y1=ax12,y2=ax22,由此利用点差法求出直线AB过定点(0,
),M点坐标是(0,
).
| 1 |
| a |
| 1 |
| a |
解答:
解:由
=λ
+μ
,且λ+μ=1,
得
=λ
+(1-λ)
,
即
=λ
,
∴A,B,M三点共线,于是问题转化为动直线过定点,
设A(x1,y1),B(x2,y2),则y1=ax12,y2=ax22,
两式相减,得y1-y2=a(x1+x2)(x1-x2),
∴kAB=
=a(x1+x2),
∴直线AB方程为y-y1=a(x1+x2)(x-x1),
即y=a(x1+x2)(x-x1)+y1=a(x1+x2)x-ax12-ax1x2+ax12=a(x1+x2)x-ax1x2,①
∵
⊥
,∴x1x2+y1y2=0,
即x1x2+ax12x22=0,∴a2x1x2=-1,②
把②代入①,得y=a(x1+x2)x+
,
∴直线AB过定点(0,
),M点坐标是(0,
).
故答案为:(0,
).
| OM |
| OA |
| OB |
得
| OM |
| OA |
| OB |
即
| BM |
| BA |
∴A,B,M三点共线,于是问题转化为动直线过定点,
设A(x1,y1),B(x2,y2),则y1=ax12,y2=ax22,
两式相减,得y1-y2=a(x1+x2)(x1-x2),
∴kAB=
| y1-y2 |
| x1-x2 |
∴直线AB方程为y-y1=a(x1+x2)(x-x1),
即y=a(x1+x2)(x-x1)+y1=a(x1+x2)x-ax12-ax1x2+ax12=a(x1+x2)x-ax1x2,①
∵
| OA |
| OB |
即x1x2+ax12x22=0,∴a2x1x2=-1,②
把②代入①,得y=a(x1+x2)x+
| 1 |
| a |
∴直线AB过定点(0,
| 1 |
| a |
| 1 |
| a |
故答案为:(0,
| 1 |
| a |
点评:本题考查满足条件的点的坐标的求法,是中档题,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
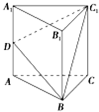 如图,在正三棱柱ABC A1B1C1中,D为棱AA1的中点,若截面三角形BC1D是面积为6的直角三角形,则此三棱柱的体积为( )
如图,在正三棱柱ABC A1B1C1中,D为棱AA1的中点,若截面三角形BC1D是面积为6的直角三角形,则此三棱柱的体积为( )A、16
| ||||
B、8
| ||||
C、4
| ||||
D、
|
 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图,如图.
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图,如图.
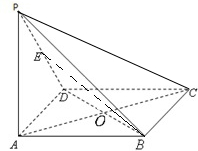 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=