题目内容
在平面直角坐标系xOy中,已知双曲线C1:2x2-y2=1.
(1)过C1的左顶点引C1的一条渐近线的平行线,求该直线与另一条渐近线及x轴围成的三角形的面积;
(2)设斜率为1的直线l交C1于P、Q两点.若l与圆x2+y2=1相切,求证:OP⊥OQ.
(1)过C1的左顶点引C1的一条渐近线的平行线,求该直线与另一条渐近线及x轴围成的三角形的面积;
(2)设斜率为1的直线l交C1于P、Q两点.若l与圆x2+y2=1相切,求证:OP⊥OQ.
考点:直线与圆锥曲线的关系,直线与圆的位置关系,双曲线的简单性质
专题:圆锥曲线中的最值与范围问题
分析:(1)双曲线C1:
-y2=1,左顶点A(-
,0),过点A与渐近线y=
x平行的直线方程为y=
x+1,由此能求出该直线与另一条渐近线及x轴围成的三角形的面积.
(2)设直线PQ的方程是y=x+b,直线PQ与已知圆相切,得b2=2,由
,得x2-2bx-b2-1=0,由此利用韦达定理结合已知条件能证明OP⊥OQ.
| x2 | ||
|
| ||
| 2 |
| 2 |
| 2 |
(2)设直线PQ的方程是y=x+b,直线PQ与已知圆相切,得b2=2,由
|
解答:
(1)解:双曲线C1:
-y2=1,左顶点A(-
,0),
渐近线方程y=±
x,
过点A与渐近线y=
x平行的直线方程为y=
(x+
),
即y=
x+1,
解方程组
,得x=-
,y=
,
∴该直线与另一条渐近线及x轴围成的三角形的面积:
S=
|OA|•|y|=
×
×
=
.
(2)证明:设直线PQ的方程是y=x+b,
∵直线PQ与已知圆相切,∴
=1,解得b2=2,
由
,得x2-2bx-b2-1=0,
设P(x1,y1),Q(x2,y2),则x1+x2=2b,x1x2=-1-b2,
又y1y2=(x1+b)(x2+b),
∴
•
=x1x2+y1y2=2x1x2+b(x1+x2)+b2
=2(-1-b2)+2b2+b2
=b2-2=0,
∴OP⊥OQ.
| x2 | ||
|
| ||
| 2 |
渐近线方程y=±
| 2 |
过点A与渐近线y=
| 2 |
| 2 |
| ||
| 2 |
即y=
| 2 |
解方程组
|
| ||
| 4 |
| 1 |
| 2 |
∴该直线与另一条渐近线及x轴围成的三角形的面积:
S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 8 |
(2)证明:设直线PQ的方程是y=x+b,
∵直线PQ与已知圆相切,∴
| |b| | ||
|
由
|
设P(x1,y1),Q(x2,y2),则x1+x2=2b,x1x2=-1-b2,
又y1y2=(x1+b)(x2+b),
∴
| OP |
| OQ |
=2(-1-b2)+2b2+b2
=b2-2=0,
∴OP⊥OQ.
点评:本题考查三角形面积的求法,考查两线段垂直的证明,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
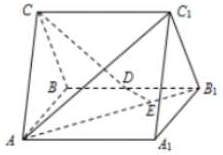 如图,直三棱柱ABC-A1B1C1中,AC=BC,C到AB的距离大于1,AA1=AB=2,D为BB1的中点,E为AB1上的一点,AE=3EB1.
如图,直三棱柱ABC-A1B1C1中,AC=BC,C到AB的距离大于1,AA1=AB=2,D为BB1的中点,E为AB1上的一点,AE=3EB1.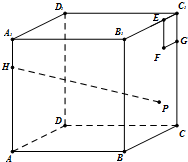 如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA1上,且HA1=1.在侧面BCC1B1内作边长为1的正方形EFGC1,P是侧面BCC1B1内一动点,且点P到平面CDD1C1距离等于线段PF的长.则当点P运动时,|HP|2的最小值是( )
如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA1上,且HA1=1.在侧面BCC1B1内作边长为1的正方形EFGC1,P是侧面BCC1B1内一动点,且点P到平面CDD1C1距离等于线段PF的长.则当点P运动时,|HP|2的最小值是( )