题目内容
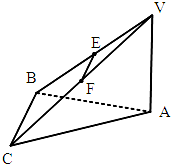 如图,在三棱锥V-ABC中,点E、F分别为VB、VC的中点.平面VAB⊥平面ABC,平面VAC⊥平面ABC.
如图,在三棱锥V-ABC中,点E、F分别为VB、VC的中点.平面VAB⊥平面ABC,平面VAC⊥平面ABC.(1)求证:EF∥平面ABC;
(2)若二面角C-VB-A为90°,且VA=BC=
| 1 |
| 2 |
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知得EF∥BC,由此能证明EF∥平面ABC.
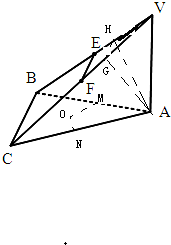
(2)在△ABC内任取一点O,作OM⊥AB于M,作ON⊥AC于N,由已知得VA⊥BC,作AH⊥VB于H,作AG⊥VC于G,连结GH,得GH⊥VC,∠AGH为二面角A-VC-B的平面角,由此能求出二面角A-VC-B的余弦值.
(2)在△ABC内任取一点O,作OM⊥AB于M,作ON⊥AC于N,由已知得VA⊥BC,作AH⊥VB于H,作AG⊥VC于G,连结GH,得GH⊥VC,∠AGH为二面角A-VC-B的平面角,由此能求出二面角A-VC-B的余弦值.
解答:
 (1)证明:∵点E,F分别为VB、VC的中点,
(1)证明:∵点E,F分别为VB、VC的中点,
∴EF∥BC,
∵BC?平面ABC,EF?平面ABC,
∴EF∥平面ABC.
(2)解:在△ABC内任取一点O,作OM⊥AB于M,
∵面VAB⊥面ABC,交线为AB,
∴OM⊥面VAB,∴VA⊥OM,
同理,作ON⊥AC于N,则VA⊥ON,
又OM∩ON=O,OM,ON?平面ABC,
∴VA⊥平面ABC,∴VA⊥BC,
作AH⊥VB于H,
∵二面角C-VB-A为90°,
∴平面VBC⊥平面VAB,交线为VB,
∴AH⊥平面VBC,∴BC⊥AH,
∵AH∩VA=A,AH,VA?平面VAB,
∴BC⊥平面VAB,∴BC⊥AB,BC⊥VB,
作AG⊥VC于G,连结GH,
由三垂线定理的逆定理,得GH⊥VC,
∴∠AGH为二面角A-VC-B的平面角,
设AC=2,由VA=BC=1,
在Rt△VAC中,AC=2,VA=1,VC=
,
∴AG=
=
,
在Rt△ABC中,AC=2,BC=1,AB=
=
,
在Rt△VAB中,VA=1,AB=
,VB=2,
AH=
=
,
在Rt△VGH中,GH=
=
,
∴cos∠AGH=
=
,
∴二面角A-VC-B的余弦值为
.
 (1)证明:∵点E,F分别为VB、VC的中点,
(1)证明:∵点E,F分别为VB、VC的中点,∴EF∥BC,
∵BC?平面ABC,EF?平面ABC,
∴EF∥平面ABC.
(2)解:在△ABC内任取一点O,作OM⊥AB于M,
∵面VAB⊥面ABC,交线为AB,
∴OM⊥面VAB,∴VA⊥OM,
同理,作ON⊥AC于N,则VA⊥ON,
又OM∩ON=O,OM,ON?平面ABC,
∴VA⊥平面ABC,∴VA⊥BC,
作AH⊥VB于H,
∵二面角C-VB-A为90°,
∴平面VBC⊥平面VAB,交线为VB,
∴AH⊥平面VBC,∴BC⊥AH,
∵AH∩VA=A,AH,VA?平面VAB,
∴BC⊥平面VAB,∴BC⊥AB,BC⊥VB,
作AG⊥VC于G,连结GH,
由三垂线定理的逆定理,得GH⊥VC,
∴∠AGH为二面角A-VC-B的平面角,
设AC=2,由VA=BC=1,
在Rt△VAC中,AC=2,VA=1,VC=
| 5 |
∴AG=
| VA•AC |
| VC |
| 2 | ||
|
在Rt△ABC中,AC=2,BC=1,AB=
| AC2-BC2 |
| 3 |
在Rt△VAB中,VA=1,AB=
| 3 |
AH=
| VA•AB |
| VB |
| ||
| 2 |
在Rt△VGH中,GH=
| AG2-AH2 |
| 1 | ||
2
|
∴cos∠AGH=
| GH |
| AG |
| 1 |
| 4 |
∴二面角A-VC-B的余弦值为
| 1 |
| 4 |
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
甲、乙两人在一次赛跑中路程s与t的函数关系如图所示,则下列说法正确的是( )
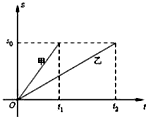

| A、甲比乙先出去 |
| B、乙比甲跑的路程多 |
| C、甲先到达终点 |
| D、甲、乙两人的速度相同 |
由不大于7的质数组成的集合是( )
| A、﹛1,2,3,5,7﹜ |
| B、﹛2,3,5,7﹜ |
| C、﹛2,3,5﹜ |
| D、﹛x|x≤7﹜ |
 如图,在△ABC中,点O是BC的中点.过点O的直线分别交直线AB,AC于不同的两点M,N,若
如图,在△ABC中,点O是BC的中点.过点O的直线分别交直线AB,AC于不同的两点M,N,若