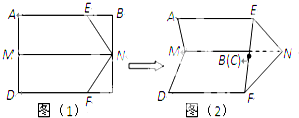
 如图(1),矩形ABCD中,M、N分别为边AD、BC的中点,E、F分别为边AB、CD上的定点且满足EB=FC,现沿MN,EN,FN折叠使点B、C重合且与E、F共线,如图(2).若此时二面角A-MN-D的大小为60°,则折叠后EN与平面MNFD所成角的正弦值是( )
如图(1),矩形ABCD中,M、N分别为边AD、BC的中点,E、F分别为边AB、CD上的定点且满足EB=FC,现沿MN,EN,FN折叠使点B、C重合且与E、F共线,如图(2).若此时二面角A-MN-D的大小为60°,则折叠后EN与平面MNFD所成角的正弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图(1),矩形ABCD中,M、N分别为边AD、BC的中点,E、F分别为边AB、CD上的定点且满足EB=FC,现沿MN,EN,FN折叠使点B、C重合且与E、F共线,如图(2).若此时二面角A-MN-D的大小为60°,则折叠后EN与平面MNFD所成角的正弦值是( )
如图(1),矩形ABCD中,M、N分别为边AD、BC的中点,E、F分别为边AB、CD上的定点且满足EB=FC,现沿MN,EN,FN折叠使点B、C重合且与E、F共线,如图(2).若此时二面角A-MN-D的大小为60°,则折叠后EN与平面MNFD所成角的正弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|