若函数f(x)=x2-4x-m+4(-1≤x<4)有两个零点,则m的取值范围是( )
| A、(0,9] |
| B、(4,9) |
| C、(0,4) |
| D、[2,4] |
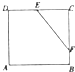 在如图所示的边长为6的正方形ABCD中,点E是DC的中点,且
在如图所示的边长为6的正方形ABCD中,点E是DC的中点,且| CF |
| 2 |
| 3 |
| CB |
| EF |
| AE |
| A、-18 | B、20 |
| C、12 | D、-15 |
| A、(0,9] |
| B、(4,9) |
| C、(0,4) |
| D、[2,4] |
 在如图所示的边长为6的正方形ABCD中,点E是DC的中点,且
在如图所示的边长为6的正方形ABCD中,点E是DC的中点,且| CF |
| 2 |
| 3 |
| CB |
| EF |
| AE |
| A、-18 | B、20 |
| C、12 | D、-15 |