题目内容
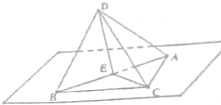 已知,如图所示的△DAB是正三角形,与等腰三角形ABC的公共边AB=2
已知,如图所示的△DAB是正三角形,与等腰三角形ABC的公共边AB=2| 3 |
(Ⅰ)当平面ABD⊥平面ABC时,求CD的长;
(Ⅱ)如果△ABC绕边AB转动,请你首先描述一下你对直线AB与CD的位置关系的直观感知,然后运用所学知识证明你的直观感知.
考点:平面与平面垂直的判定,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(Ⅰ)取AB中点为E,连DE,CE,由AB⊥DE,AB⊥CE,可证平面ABD⊥平面ABC,从而有DE⊥EC,由勾股定理可求CD的长;
(Ⅱ)由(Ⅰ)知AB⊥DE,AB⊥CE,可证AB⊥平面EDC,即可证明始终有AB⊥CD.
(Ⅱ)由(Ⅰ)知AB⊥DE,AB⊥CE,可证AB⊥平面EDC,即可证明始终有AB⊥CD.
解答:
解:(Ⅰ)取AB中点为E,连DE,CE,
∵△DAB是正三角形,
∴AB⊥DE,
又∵△BCA是∠ACB=120°的等腰三角形,
∴AB⊥CE,
∵平面ABD⊥平面ABC,
∴ED⊥平面ABC,即DE⊥EC,
∵DE=3,CE=1,
∴CD=
,
(Ⅱ)当△ABD绕AB转动时,AB始终与CD垂直,
由(Ⅰ)知AB⊥DE,AB⊥CE,
∴AB⊥平面EDC,CD?平面EDC,
∴AB⊥CD,
∴当△ABD绕AB转动时,AB始终与CD垂直.
∵△DAB是正三角形,
∴AB⊥DE,
又∵△BCA是∠ACB=120°的等腰三角形,
∴AB⊥CE,
∵平面ABD⊥平面ABC,
∴ED⊥平面ABC,即DE⊥EC,
∵DE=3,CE=1,
∴CD=
| 10 |
(Ⅱ)当△ABD绕AB转动时,AB始终与CD垂直,
由(Ⅰ)知AB⊥DE,AB⊥CE,
∴AB⊥平面EDC,CD?平面EDC,
∴AB⊥CD,
∴当△ABD绕AB转动时,AB始终与CD垂直.
点评:本题主要考察了平面与平面垂直的判定,空间中直线与直线之间的位置关系,属于中档题.

练习册系列答案
相关题目
点O在△ABC的内部,且满足
+2
+4
=0,则△ABC的面积与△AOC的面积之比是( )
| OA |
| OB |
| OC |
A、
| ||
| B、3 | ||
C、
| ||
| D、2 |
某足够大的长方体箱子内放置一球O,已知球O与长方体一个顶点出发的三个平面都相切,且球面上一点M到三个平面的距离分别为3,2,1,则此半球的半径为( )
A、3+2
| ||||
B、3-
| ||||
C、3+
| ||||
D、3+2
|