题目内容

设m∈[-5，5]，则方程x2+mx+
m+2
4
=0没有实数根的概率是
 
．
考点：几何概型
专题：计算题,概率与统计
分析：根据题意先确定是几何概型中的长度类型，由方x2+mx+
m+2
4
=0没有实数根，则必须有△＜0，计算出区间的长度，区间[-5，5]的长度，代入几何概型概率计算公式，即可得到答案．
解答： 解：∵方程x2+mx+
m+2
4
=0没有实数根，
∴△＜0，得到m2-m-2＜0
∴-1＜m＜2，区间长度为3，
∵m∈[-5，5]，区间长度为10，
∴所求概率为
3
10
．
故答案为：
3
10
．
点评：本题主要考查几何概型的概率计算．其中根据已知条件计算出基本事件总数对应的几何量的大小，和满足条件的几何量的大小是解答本题的关键．
练习册系列答案
相关题目
一个盒子中装有大小完全相同且分别标有字母a，b的2个黄球和分别标有字母c，d的2个红球．
（Ⅰ）如果每次任取1个球，取出后不放回，连续取两次，求取出的两个球中恰有一个是黄球的概率；
（Ⅱ）如果每次任取1个球，取出后放回，连续取两次，求取出的两个球中至多有一个是黄球的概率．
已知双曲线C：
x2
a2
-
y2
b2
=1的左、右焦点分别是F1，F2，正三角形AF1F2的一边AF1与双曲线左支交于点B，且
AF1
=4
BF1
，则双曲线C的离心率的值是
 
．
数列{
n
an
}的前n项和Sn为
 
．
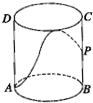如图，有一圆柱形的开口容器（下表面密封），其轴截面是边长为4的正方形，P是BC中点，现有一只蚂蚁位于外壁外处，内壁P处有一米粒，则这只蚂蚁取得米粒所需经过的最短路程为
 
．
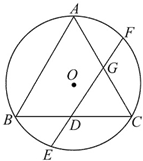如图，△ABC是⊙O的内接正三角形，弦EF经过BC的中点D，且EF∥AB，若AB=2，则DE的长是
 
．
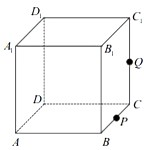平面内有n条直线，其中任何两条不平行，任何三条不共点，当n=k时把平面分成的区域数记为f（k），则n=k+1时f（k+1）=f（k）+
 
．
如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S．则下列命题正确的是
 
（写出所有正确命题的编号）．
①当0＜CQ＜
1
2
时，S为四边形；
②当CQ=
1
2
时，S不为等腰梯形；
③当CQ=
3
4
时，S与C1D1的交点R满足C1R=
1
3
；
④当
3
4
＜CQ＜1时，S为六边形；
⑤当CQ=1时，S的面积为
6
2
．
函数f（x）=x3+x-1在（0，4）上零点的个数为（　　）
A、0B、1C、2D、3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网