题目内容
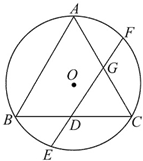 如图,△ABC是⊙O的内接正三角形,弦EF经过BC的中点D,且EF∥AB,若AB=2,则DE的长是
如图,△ABC是⊙O的内接正三角形,弦EF经过BC的中点D,且EF∥AB,若AB=2,则DE的长是考点:与圆有关的比例线段
专题:立体几何
分析:由相交弦定理得DE•DF=BD•CD=1,EG•FG=AG•CG=1.又DG=
AB=1,由此能求出结果.
| 1 |
| 2 |
解答:
解:∵△ABC是⊙O的内接正三角形,弦EF经过BC的中点D,
且EF∥AB,AB=2,
∴由相交弦定理得DE•DF=BD•CD=1,
同理EG•FG=AG•CG=1.又DG=
AB=1,
∴DE(1+FG)=1,FG(1+DE)=1,
∴DE=FG=
.
答案:
.
且EF∥AB,AB=2,
∴由相交弦定理得DE•DF=BD•CD=1,
同理EG•FG=AG•CG=1.又DG=
| 1 |
| 2 |
∴DE(1+FG)=1,FG(1+DE)=1,
∴DE=FG=
| ||
| 2 |
答案:
| ||
| 2 |
点评:本题考查线段长的求法,解题时要认真审题,注意相交弦定理的合理运用.

练习册系列答案
相关题目
已知函数f(x)=
,若方程f(x)-kx=0恰有两个不同的实根时,则实数k的取值范围是(其中e为自然对数的底数)( )
|
| A、(1,e) |
| B、[1,3] |
| C、(3,+∞) |
| D、(e,3] |
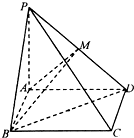 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,点M是PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,点M是PD的中点.