题目内容
一个盒子中装有大小完全相同且分别标有字母a,b的2个黄球和分别标有字母c,d的2个红球.
(Ⅰ)如果每次任取1个球,取出后不放回,连续取两次,求取出的两个球中恰有一个是黄球的概率;
(Ⅱ)如果每次任取1个球,取出后放回,连续取两次,求取出的两个球中至多有一个是黄球的概率.
(Ⅰ)如果每次任取1个球,取出后不放回,连续取两次,求取出的两个球中恰有一个是黄球的概率;
(Ⅱ)如果每次任取1个球,取出后放回,连续取两次,求取出的两个球中至多有一个是黄球的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)分别求出取出的两个球中恰有一个是黄球的事件的个数、所有可能的情况的个数,前者除以后者即可求出取出的两个球中恰有一个是黄球的概率;
(Ⅱ)首先求出取出的两个球都是黄球的概率,用1减去取出的两个球都是黄球的概率,求出取出的两个球中至多有一个是黄球的概率即可.
(Ⅱ)首先求出取出的两个球都是黄球的概率,用1减去取出的两个球都是黄球的概率,求出取出的两个球中至多有一个是黄球的概率即可.
解答:
解:(Ⅰ)第一次、第二次取到黄球的事件的个数都是:2×2=4(个)
取出的两个球中恰有一个是黄球的事件的个数为4+4=8(个),
连续取两次,所有可能的情况的个数为4×3=12(个),
所有取出的两个球中恰有一个是黄球的概率是
=
.
(Ⅱ)取出的两个球都是黄球的概率:
=
,
所以取出的两个球中至多有一个是黄球的概率:
1-
=
.
取出的两个球中恰有一个是黄球的事件的个数为4+4=8(个),
连续取两次,所有可能的情况的个数为4×3=12(个),
所有取出的两个球中恰有一个是黄球的概率是
| 8 |
| 12 |
| 2 |
| 3 |
(Ⅱ)取出的两个球都是黄球的概率:
| 2×2 |
| 4×4 |
| 1 |
| 4 |
所以取出的两个球中至多有一个是黄球的概率:
1-
| 1 |
| 4 |
| 3 |
| 4 |
点评:此题主要考查了古典概型及其概率计算公式的运用,解答此题的关键是要弄清楚:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| P(m) |
| P(n) |

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
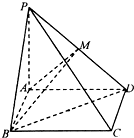 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,点M是PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,点M是PD的中点.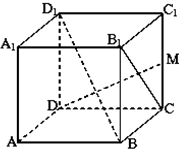 如图,正方体ABCD-A1B1C1D1中,M是CC1的中点;
如图,正方体ABCD-A1B1C1D1中,M是CC1的中点; 在长方体ABCD-A1B1C1D1中,E为AA1的中点,AB=BC=1,AA1=2.
在长方体ABCD-A1B1C1D1中,E为AA1的中点,AB=BC=1,AA1=2.