题目内容
平面内有n条直线,其中任何两条不平行,任何三条不共点,当n=k时把平面分成的区域数记为f(k),则n=k+1时f(k+1)=f(k)+ .
考点:归纳推理
专题:推理和证明
分析:首先判断1条直线,将平面分成2个区域,即f(1)=2;2条直线,将平面分成4个区域,即f(2)=4;f(3)=7,f(4)=11,f(5)=16,每一项与它前面一项的差构成一个等差数列,据此解答即可.
解答:
解:f(1)=2,f(2)=4,f(3)=7,f(4)=11,f(5)=16…,
f(2)-f(1)=4-2=2
f(3)-f(2)=7-4=3
f(4)-f(3)=11-7=4
f(5)-f(4)=16-11=5
…
归纳推理,得出f(n)-f(n-1)=n,f(n)=f(n-1)+n,
所以n=k+1时f(k+1)=f(k)+(k+1).
故答案为:k+1.
f(2)-f(1)=4-2=2
f(3)-f(2)=7-4=3
f(4)-f(3)=11-7=4
f(5)-f(4)=16-11=5
…
归纳推理,得出f(n)-f(n-1)=n,f(n)=f(n-1)+n,
所以n=k+1时f(k+1)=f(k)+(k+1).
故答案为:k+1.
点评:本题主要考查了归纳推理的灵活运用,考查了数列的递推式,解答此题的关键是分析出每一项与它前面一项的差构成一个等差数列.

练习册系列答案
相关题目
下列命题中,真命题是( )
| A、?x0∈R,sinx0+cosx0=3 |
| B、?x∈(0,π),cosx>0 |
| C、?x0∈R,x20+x0+1=0 |
| D、?x∈(0,+∞),ex>1+x |
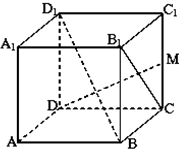 如图,正方体ABCD-A1B1C1D1中,M是CC1的中点;
如图,正方体ABCD-A1B1C1D1中,M是CC1的中点;