题目内容
已知双曲线C:
-
=1的左、右焦点分别是F1,F2,正三角形AF1F2的一边AF1与双曲线左支交于点B,且
=4
,则双曲线C的离心率的值是 .
| x2 |
| a2 |
| y2 |
| b2 |
| AF1 |
| BF1 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出F1(-c,0),A(0,
c),设B(x,y),根据
=4
,可得x=-
c,y=
c,代入双曲线方程,即可得出结论.
| 3 |
| AF1 |
| BF1 |
| 3 |
| 4 |
| ||
| 4 |
解答:
解:由题意,F1(-c,0),A(0,
c),
设B(x,y),则
∵
=4
,
∴(-c,-
c)=4(-c-x,-y),
∴x=-
c,y=
c,
代入双曲线方程,化简可得,9e4-28e2+16=0,
∴e=
.
故答案为:
.
| 3 |
设B(x,y),则
∵
| AF1 |
| BF1 |
∴(-c,-
| 3 |
∴x=-
| 3 |
| 4 |
| ||
| 4 |
代入双曲线方程,化简可得,9e4-28e2+16=0,
∴e=
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查双曲线的几何性质,考查向量知识的运用,考查学生的计算能力,确定坐标之间的关系是关键.

练习册系列答案
相关题目
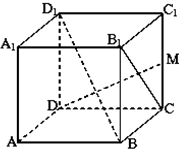 如图,正方体ABCD-A1B1C1D1中,M是CC1的中点;
如图,正方体ABCD-A1B1C1D1中,M是CC1的中点; 在长方体ABCD-A1B1C1D1中,E为AA1的中点,AB=BC=1,AA1=2.
在长方体ABCD-A1B1C1D1中,E为AA1的中点,AB=BC=1,AA1=2.