题目内容

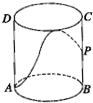如图，有一圆柱形的开口容器（下表面密封），其轴截面是边长为4的正方形，P是BC中点，现有一只蚂蚁位于外壁外处，内壁P处有一米粒，则这只蚂蚁取得米粒所需经过的最短路程为
 
．
考点：多面体和旋转体表面上的最短距离问题
专题：计算题,空间位置关系与距离
分析：画出圆柱的侧面展开图，根据对称性，求出AQ+PQ的最小值就是AE的长，求解即可．
解答： 解：侧面展开后得矩形ABCD，其中AB=π，AD=4问题转化为在CD上找一点Q，
使AQ+PQ最短作P关于CD的对称点E，连接AE，
令AE与CD交于点Q，则得AQ+PQ的最小值就是AE为
(2π)2+62
=2
π2+9
．
故答案为：2
π2+9
．
点评：本题考查求曲面上最短路程问题，通常考虑侧面展开，考查转化思想，计算能力，是基础题．
练习册系列答案
相关题目
两台机床同时生产一种零件，在10天中，两台机床每天的次品数如下：
甲　1，0，2，0，2，3，0，4，1，2
乙　1，3，2，1，0，2，1，1，0，1
（1）哪台机床次品数的平均数较小？
（2）哪台机床的生产状况比较稳定？
已知原命题为“若a＞2，则a2＞4”，写出它的逆命题、否命题、逆否命题，并判断四种命题的真假．
4张卡片的正、反两面分别写有数字0，1；2，3；4，5；6，7，将这4张卡片排成一排，可构成
 
个不同的四位偶数．
复数（3-i）m-（1+i）对应的点在第三象限内，则实数m的取值范围是
 
．
设m∈[-5，5]，则方程x2+mx+
m+2
4
=0没有实数根的概率是
 
．
在Rt△ABC中，若∠C=90°，AC=b，BC=a，斜边AB上的高为h，则有结论h2=
a2b2
a2+b2
，运用类比方法，若三棱锥的三条侧棱两两互相垂直且长度分别为a，b，c，且三棱锥的直角顶点到底面的高为h，则有结论：
 
．
若关于x的不等式x2+|x3-2x2|≥ax-4在x∈[1，10]内恒成立，则实数a的取值范围是
 
．
A
3
n
=
C
4
n
，则n=（　　）
A、26B、27C、28D、29

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网